- 2.2. Расчёт в табличной форме
- П.3. Табличный метод расчёта параметров сетевого графика.
- 33. Табличный метод расчета аналитических параметров сетевой модели.
- 34. Расчет сетевой модели методом диагональной таблиц
- 35. Секторный метод расчетов сетевой модели
- Табличный метод расчета параметров сетевого графика
2.2. Расчёт в табличной форме
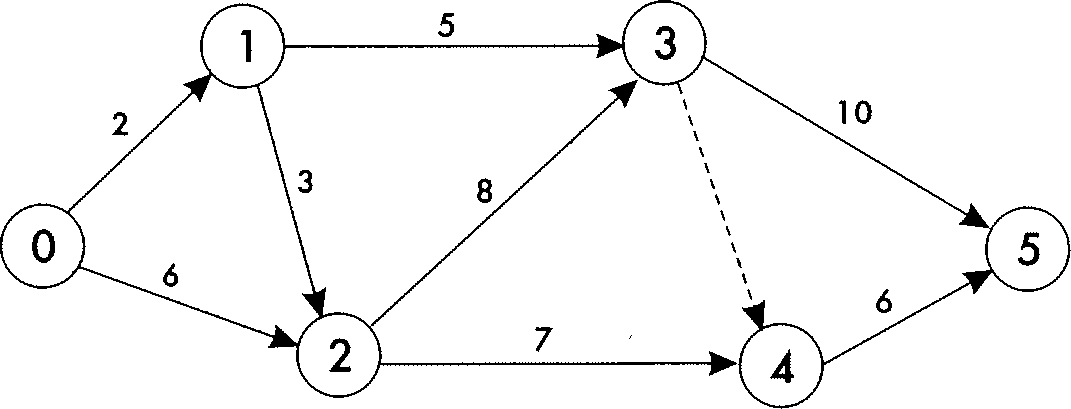
Рассмотрим методику расчёта сетевого графика, приведённом на рисунке 10.
Табличный способ является универсальным и характеризуется большой наглядностью. Для расчёта сетевого графика в табличной форме события должны быть пронумерованы таким образом, чтобы номер начального события был меньше номера конечного события работы.
На первом этапе на основании составленной сетевой модели заполняются первые три графы (см. таблицу 2): номера начальных событий предшествующих работ (графа 1); шифр данной работы (графа 2); продолжительность работы (графа 3). Заполнение следует начинать со второй графы, придерживаясь правила: сначала записываются все работы, выходящие из первого события, затем из второго и далее в порядке нарастания номеров. Одновременно с записью работ, выходящих из одного события, заполняются первая и третья графы таблицы.
На втором этапе рассчитываются ранние сроки начала и окончания работ (графы 4 и 5). Заполнение их ведётся построчно, начиная с исходного события до завершающего.
Ранние начала исходных работ всегда равны нулю, затем определяются ранние окончания этих работ по формуле (2). Так, раннее окончание работы 1-2 будет: 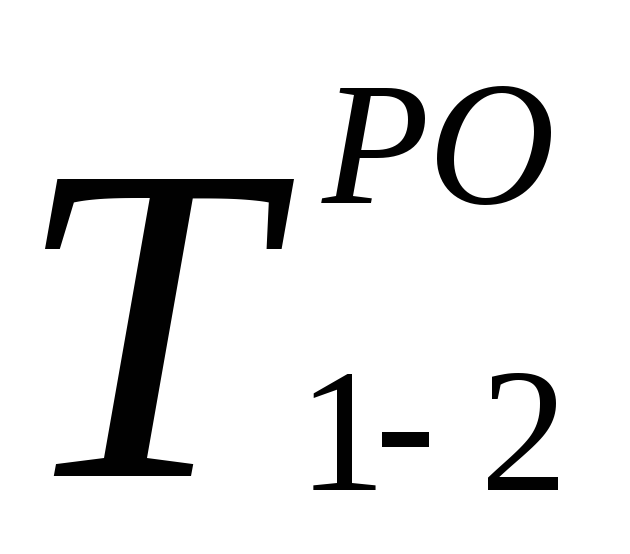
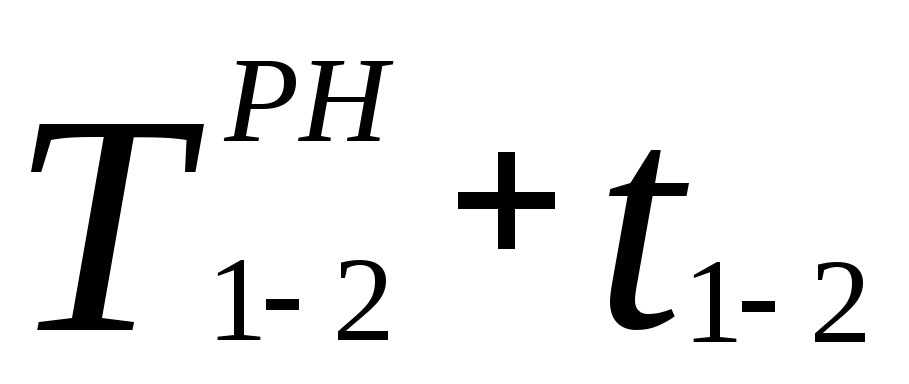
Дальнейшее заполнение граф 4 и 5 осуществляется последовательно сверху вниз, при этом ранее начало последующих работ определяется по формуле (1). Например, раннее начало работы 2-3 равно 7, а для работы 5-6 раннее начало равно 13 – максимальному из ранних окончаний предшествующих работ 3-5 и 4-5.
Раннее начало завершающего события равно продолжительности критического пути, которая в рассматриваемом примере равна 24 дням.
На третьем этапе производится расчёт поздних начал и окончаний работ (заполняются соответственно графы 6 и 7). Расчёт ведётся от завершающего события к исходному (снизу вверх).
Позднее окончание завершающих работ равно продолжительности критического пути (для работы 9-10 – 24 дня). Поздние начала работ определяются по формуле (5). Так, для работы 9-10 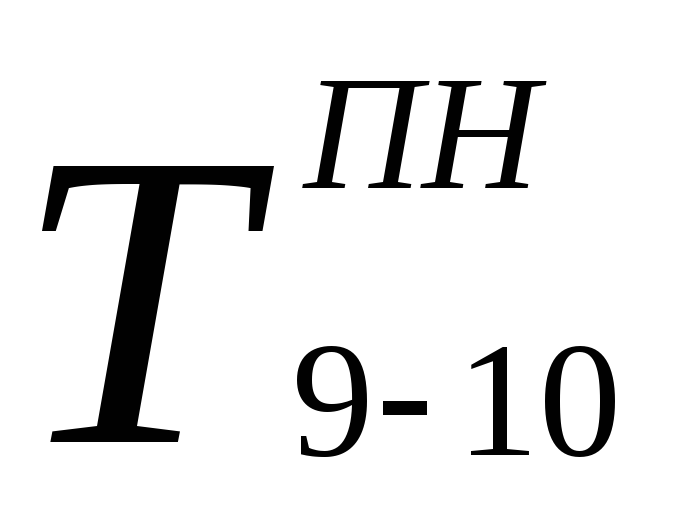
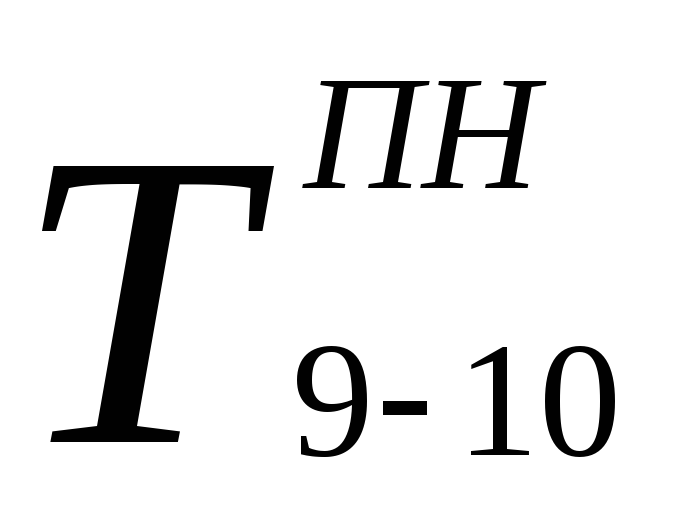
Т а б л и ц а 2 – Расчёт графика в табличной форме
Номера начальных событий предшествующих работ
П.3. Табличный метод расчёта параметров сетевого графика.
Пример: Определить временные параметры сетевого графика, пользуясь табличным методом.
Все вычисления будем заносить в таблицу. Перечень работ и их продолжительность переносим во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.
В первой графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа. Так, для работы (5,10) в графу 1 поставим число 2, т.к. на номер 5 оканчиваются 2 работы: (1,5) и (3,5). Количество предшествующих работ для исходного события равно 0.
Графа 3 заполняется на основе сетевого графика или перечня работ с временными оценками.
Далее заполняем графы 4 и 5. Для работ, имеющих цифру 0 в графе 1, в графу 4 также заносятся нули, а их значения в графе 5 получаются в результате суммирования граф 3 и 4 (по формуле (4)). В нашем случае для работ (1,2), (1,3), (1,5) в графе 4 ставим 0, а в графе 5 – 0+5=5, 0+7=7, 0+4=4. Для заполнения следующих строк графы 4, т.е. строк начиная с номера 2, просматриваются заполненные строки графы 5, содержащие работы, которые оканчиваются на этот номер, и максимальное значение переносится в графу 4 обрабатываемых строк. В данном случае такая работа одна – (1,2). Цифру 5 из графы 5 переносим в графу 4 для всех работ, начиная с номера 2, т.е. в две последующие строки с номерами (2,4) и (2,6). Для каждой из этих работ путём суммирования граф 3 и 4 сформируем значение графы 5: tр.о.(2,4)=0+5=5, tр.о.(2,6)=8+5=13. Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы.
Код работы (i,j)
Продолжительность работы t(i,j)
tро(i,j)
33. Табличный метод расчета аналитических параметров сетевой модели.
Существует большое количество алгоритмов расчета сетевых графиков как ручным, так и автоматизированным способом. Любой программный пакет по календарному планированию проекта ческие параметры любого сетевого графика. Но знание «ручных» технологий позволяет лучше понять взаимосвязь между этими показателями и использовать сетевые модели без каких-либо специализированных программ.
Итак, рассчитаем параметры сетевой модели табличным методом. Воспользуемся тем же сетевым графиком, на примере которого мы рассчитывали аналитические параметры в предыдущих параграфах (см. рис. 5.37). Для этого воспользуемся табл. 5.2.
В графу 1 вносится количество работ, предшествующих рассчитываемой, в графу 2 — номера начальных событий рассчитываемых работ, в графу 3 — номера конечных событий рассчитываемых работ, в графу 4 — ранние начала работ, в графу 5 — продолжительности выполнения работ, в графу 6 — ранние окончания работ, в графу 7 — поздние окончания работ, в графу 8 — продолжительности выполнения работ, в графу 9 — поздние начала работ, в графу 10 — общие резервы работ, в графу 11 — частные резервы работ.
Графы 1, 2, 3, 5 и 8 заполняются данными из сетевого графика. Затем сверху вниз заполняются графы в таком порядке: 4 и 6, 7 и 9, 10, 11.
34. Расчет сетевой модели методом диагональной таблиц
Расчет сетевого графика методом диагональной таблицы (иногда этот метод называют матричным) ведется с ориентацией на события, а не на работы. В начале вычерчивается квадратная сетка, в которой число строк и число граф равно числу событий графика Затем слева, сверху вниз, проставляются все номера начальных событий (индекс i), а вверху слева направо — номера конечных событий (индекс j). В ячейках на пересечении начального и конечного событий проставляются значения продолжительности работ.
Из таблицы cправа видно, сколько и какие работы из событий выходят и сколько и какие работы в события входят. Так, из события 2 выходят две работы — 2—3 и 2—4, продолжительность которых 8 и 7 дней соответственно, а в событие 5 входят две работы — 3—5 и 4—5 продолжительностью 10 и 6 дней соответственно. При правильном заполнении таблицы значения продолжительности работ должны образовать диагонали.
35. Секторный метод расчетов сетевой модели
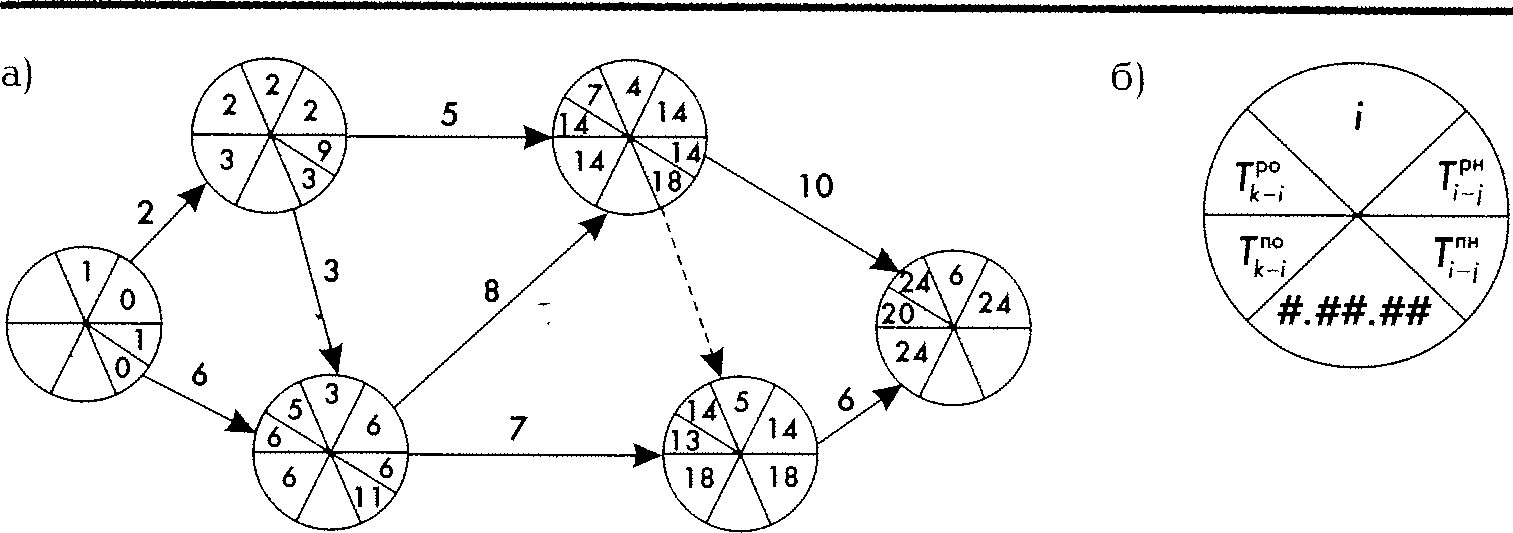
Для изучения секторного метода рассмотрим сетевой график, изображенный на
Как видно из рисунка, секторный метод предполагает изображение сетевого графика с увеличенными кружками, разделенными на шесть секторов, которые в дальнейшем могут разбиваться на подсекторы. В верхнем центральном секторе ставится номер события, в нижнем — календарная дата начала работ. В два верхних боковых сектора вносятся ранние начала и окончания работ, а в два боковых нижних — соответственно поздние начала и окончания работ. Слева принято записывать окончания работ, входящих в данное событие, справа — начала работ, выходящих из данного события.
Расчет показателей графика ведется двумя проходами: прямым от исходного события до завершающего последовательно по всем путям графика и обратным — от завершающего события до исходного. При прямом проходе определяются ранние начала и окончания работ. При обратном проходе — поздние начала и окончания работ.
Табличный метод расчета параметров сетевого графика
Пример . Определить временные параметры сетевого графика на рисунке, пользуясь табличным методом.
Решение проводим через калькулятор: все вычисления будем заносить в таблицу 3.
Перечень работ и их продолжительность перенесем во вторую и третью графы. При этом работы следует записывать в графу 2 последовательно: сначала начиная с номера 1, затем с номера 2 и т.д.
В первой графе поставим число, характеризующее количество непосредственно предшествующих работ (КПР) тому событию, с которого начинается рассматриваемая работа. Так, для работы (5,10) в графу 1 поставим число 2, т.к. на номер 5 оканчиваются 2 работы: (1,5) и (3,5).
Таблица 3 – Табличный метод расчета сетевого графика
| КПР | Код Работы | Продолжительность работы | Ранние сроки | Поздние сроки | Резервы времени | |||||||||||
| (i,j) | t(i,j) | tрн(i,j) | tро(i,j) | tпн(i,j) | tпо(i,j) | Rп | Rс | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||
| 1 | 2 | 3 | 4 | 5=3+4 | 6=7-3 | 7 | 8 | 9 | ||||||||
| 0 | (1,2) | 5 | 0 | 5 | 2 | 7 | 2 | 0 | ||||||||
| 0 | (1,3) | 7 | 0 | 7 | 0 | 7 | 0 | 0 | ||||||||
| 0 | (1,5) | 4 | 0 | 4 | 11 | 15 | 11 | 3 | ||||||||
| 1 | (2,4) | 0 | 5 | 5 | 7 | 7 | 2 | 2 | ||||||||
| 1 | (2,6) | 8 | 5 | 13 | 12 | 20 | 7 | 0 | ||||||||
| 1 | (3,4) | 0 | 7 | 7 | 7 | 7 | 0 | 0 | ||||||||
| 1 | (3,5) | 0 | 7 | 7 | 15 | 15 | 8 | 0 | ||||||||
| 1 | (3,8) | 7 | 7 | 14 | 13 | 20 | 6 | 0 | ||||||||
| 1 | (3,9) | 11 | 7 | 18 | 12 | 23 | 5 | 1 | ||||||||
| 2 | (4,7) | 12 | 7 | 19 | 7 | 19 | 0 | 0 | ||||||||
| 2 | (5,10) | 5 | 7 | 12 | 15 | 20 | 8 | 2 | ||||||||
| 1 | (6,11) | 7 | 13 | 20 | 20 | 27 | 7 | 7 | ||||||||
| 1 | (7,9) | 0 | 19 | 19 | 23 | 23 | 4 | 0 | ||||||||
| 1 | (7,11) | 8 | 19 | 27 | 19 | 27 | 0 | 0 | ||||||||
| 1 | (8,9) | 0 | 14 | 14 | 23 | 23 | 9 | 5 | ||||||||
| 1 | (8,10) | 0 | 14 | 14 | 20 | 20 | 6 | 0 | ||||||||
| 1 | (8,11) | 4 | 14 | 18 | 23 | 27 | 9 | 9 | ||||||||
| 3 | (9,11) | 4 | 19 | 23 | 23 | 27 | 4 | 4 | ||||||||
| 2 | (10,11) | 7 | 14 | 21 | 20 | 27 | 6 | 6 | ||||||||
Далее заполняем графы 4 и 5. Для работ, имеющих цифру 0 в графе 1, в графу 4 также заносятся нули, а их значения в графе 5 получаются в результате суммирования граф 3 и 4 (по формуле (2.4)). В нашем случае для работ (1,2), (1,3), (1,5) в графе 4 ставим 0, а в графе 5 — 0+5=5, 0+7=7, 0+4=4. Для заполнения следующих строк графы 4 , т.е. строк начиная с номера 2, просматриваются заполненные строки графы 5, содержащие работы, которые оканчиваются на этот номер, и максимальное значение переносится в графу 4 обрабатываемых строк. В данном случае такая работа одна — (1,2). Цифру 5 из графы 5 переносим в графу 4 для всех работ, начиная с номера 2, т.е. в две последующие строки с номерами (2,4) и (2,6). Для каждой из этих работ путем суммирования значений граф 3 и 4 сформируем значение графы 5: tр.о.(2,4)=0+5=5, tр.о.(2,6)=8+5=13. Этот процесс повторяется до тех пор, пока не будет заполнена последняя строка таблицы.
Графы 6 и 7 заполняются “обратным ходом”, т.е. “снизу вверх”. Для этого просматриваются строки, оканчивающиеся на номер последнего события, и из графы 5 выбирается максимальная величина, которая записывается в графу 7 по всем строчкам, оканчивающимся на номер последнего события (т.к. tр(i)= tп(i)). В нашем случае t(11)=27 . Затем для этих строчек находится содержание графы 6 как разности граф 7 и 3 по формуле (2.7). Далее просматриваются строки, оканчивающиеся на номер предпоследнего события, т.е. 10. Для определения графы 7 этих строк (работы (8,10) и (5,10)) просматриваются все строчки, начинающиеся с номера 10. В графу 6 среди них выбирается минимальная величина, которая переносится в графу 7 по обрабатываемым строчкам. В нашем случае она одна — (10,11), поэтому заносим в строчки (8,10) и (5,10) графы 7 цифру 20. Процесс повторяется до тех пор, пока не будут заполнены все строчки по графам 6 и 7.
Содержимое графы 8 равно разности граф 6 и 4 или граф 7 и 5 (формула (2.8).
Содержимое графы 9 вычисляется по формуле (2.9):
Rс(3,9)= tр.н(9,11)- tр.о.(3,9)=19-18=1.
Учитывая, что резерв времени имеют только события и работы, которые принадлежат критическому пути, получаем критический путь (1,3,4,7,11).
| Работа (i,j) | Количество предшествующих работ | Продолжительность tij | Сроки выполнения работ | Резервы времени | |||||
| ранние | поздние | работ | событий Rj | ||||||
| начало tij Р.Н. | окончание tij Р.О. | начало tij П.Н. | окончание tij П.О. | полный tij П | свободный tij С.В. | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| (0,1) | 0 | 15 | 0 | 15 | 0 | 15 | 0 | 0 | 0 |
| (1,2) | 1 | 16 | 15 | 31 | 15 | 31 | 0 | 0 | 0 |
| (1,3) | 1 | 6 | 15 | 21 | 22 | 28 | 7 | 0 | 7 |
| (2,4) | 1 | 6 | 31 | 37 | 31 | 37 | 0 | 0 | 0 |
| (3,5) | 1 | 5 | 21 | 26 | 28 | 33 | 7 | 0 | 7 |
| (4,6) | 1 | 8 | 37 | 45 | 37 | 45 | 0 | 0 | 0 |
| (5,6) | 1 | 6 | 26 | 32 | 39 | 45 | 13 | 13 | 0 |
| (5,7) | 1 | 8 | 26 | 34 | 35 | 43 | 9 | 0 | 9 |
| (5,8) | 1 | 14 | 26 | 40 | 33 | 47 | 7 | 7 | 0 |
| (6,8) | 2 | 2 | 45 | 47 | 45 | 47 | 0 | 0 | 0 |
| (7,8) | 1 | 4 | 34 | 38 | 43 | 47 | 9 | 9 | 0 |
| (8,9) | 3 | 3 | 47 | 50 | 47 | 50 | 0 | 0 | 0 |
а) графы 1 и 3 заполняются на основе исходных данных.
б) в графе 2 записывается количество предшествующих работ по сетевому графику или определяется из графы 1 по числу работ, имеющих второй цифрой в коде ту, с которой начинается данная работа.
г) в графе 4 раннее начало работ, выходящих из исходного события, а раннее окончание этих работ равно их продолжительности (гр. 5). Раннее начало последующих работ определяется путем выбора максимального из сроков раннего окончания предшествующих работ. Количество сравниваемых сроков равно количеству предшествующих работ графы 2. Раннее начало последующих работ можно определить после того, как найдено раннее окончание предшествующих. В свою очередь раннее окончание каждой работы находится как сумма величин раннего начала и продолжительности данной работы;
г) продолжительность критического пути определяется после заполнения граф 4 и 5 как максимальная величина из сроков раннего окончания работ, которые ведут к завершающему событию 9;
д) найденная величина критического пути ТKP дням заносится в графу 7 для всех работ, ведущих к завершающему событию. Затем заполнение ведется снизу вверх. Находятся все работы, следующие за рассматриваемой, и определяются разности между поздним окончанием этих работ и их продолжительностями. Минимальная из величин заносится в графу 7;
е) в графе 6 позднее начало работы определяется как разность позднего окончания этих работ и их продолжительности (из значений графы 7 вычитаются данные графы 3);
ж) в графе 8 полный резерв времени работы определяется разностью между значениями граф 7 и 5. Если он равен нулю, то работа является критической;
з) в графе 10 резерв времени событий j определяется как разность позднего окончания работы, заканчивающегося событием j графы 7, и ранним началом работы, начинающимся событием j;
и) значение свободного резерва времени работы определяется как разность значений графы 10 и данных графы 8 и указывает на расположение резервов, необходимых для оптимизации.