Представления и топологии сетей
Сетевые архитекторы и администраторы должны уметь показать, как будут выглядеть их сети. Они должны иметь возможность легко видеть, какие компоненты подключаются к другим компонентам, где они будут расположены и как они будут подключены. Для представления различных устройств и каналов, из которых состоит сеть, на схемах сетей часто используются символы, такие как на рисунке.
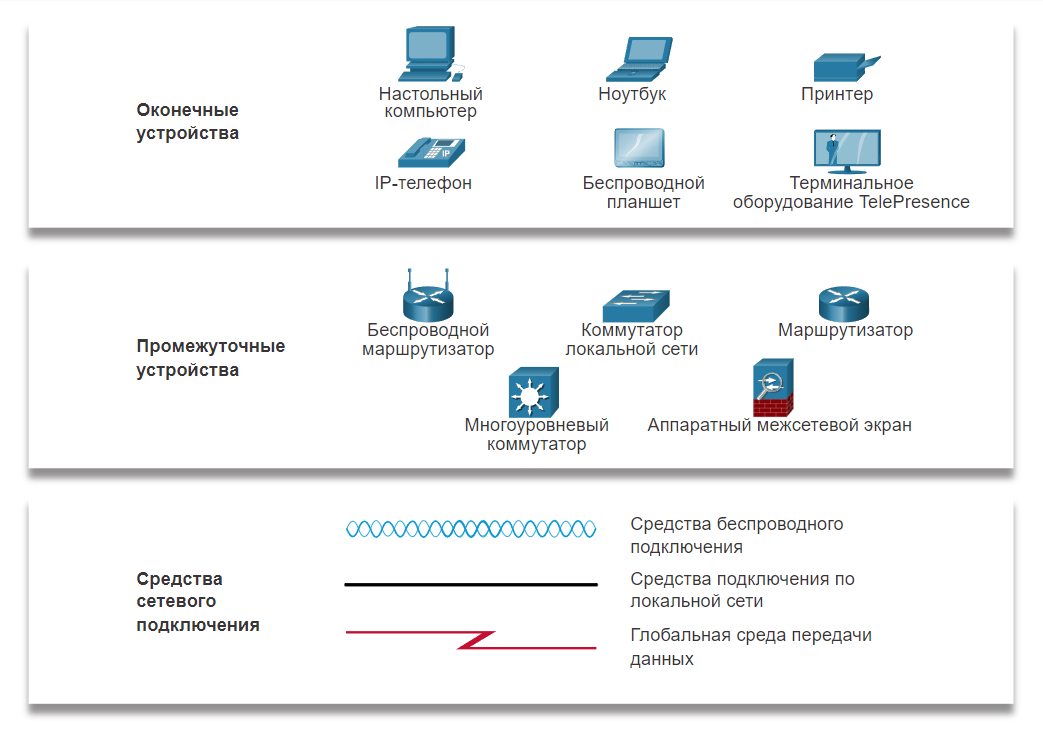
Изображение показывает символы, используемые в схемах сети. Вверху находятся следующие конечные устройства: настольный компьютер, ноутбук, принтер, IP-телефон, беспроводной стол и конечная точка TelePresence. Посередине находятся следующие промежуточные устройства: беспроводной маршрутизатор, коммутатор локальной сети, маршрутизатор, многоуровневый коммутатор и устройство межсетевого экрана. Внизу расположены следующие сетевые средства массовой информации: синие волны, изображающие беспроводные носители, сплошная черная линия, изображающая носители локальной сети, и красный световой болт, изображающий носители глобальной сети.
Схема обеспечивает наглядный способ понимания, каким образом устройства в большой сети связаны между собой. Этот тип изображения сети называется схемой топологии. Способность понимать логические представления физических сетевых компонентов имеет критическое значение в визуализации организации и функционирования сети.
В дополнение к этим представлениям используется специальная терминология для описания того, как каждое из этих устройств и носители соединяются друг с другом:
- Сетевые интерфейсные платы (Network Interface Card, NIC) служат для подключения устройства к сети.
- Физический порт — разъем на сетевом устройстве, через который кабели подключены к компьютеру или другому сетевому устройству.
- Интерфейс — специализированные порты в сетевом устройстве, которые подключаются к отдельным сетям. Поскольку маршрутизаторы используются для связывания сетей, порты маршрутизатора называются сетевыми интерфейсами.
Примечание: Термины «порт» и «интерфейс» часто взаимозаменяемы.
Топологические схемы
Диаграммы топологии являются обязательной документацией для всех, кто работает с сетью. Они представляют визуальную карту соединений в сети. Существует два типа топологических диаграмм: физические и логические.
Диаграмма физической топологии
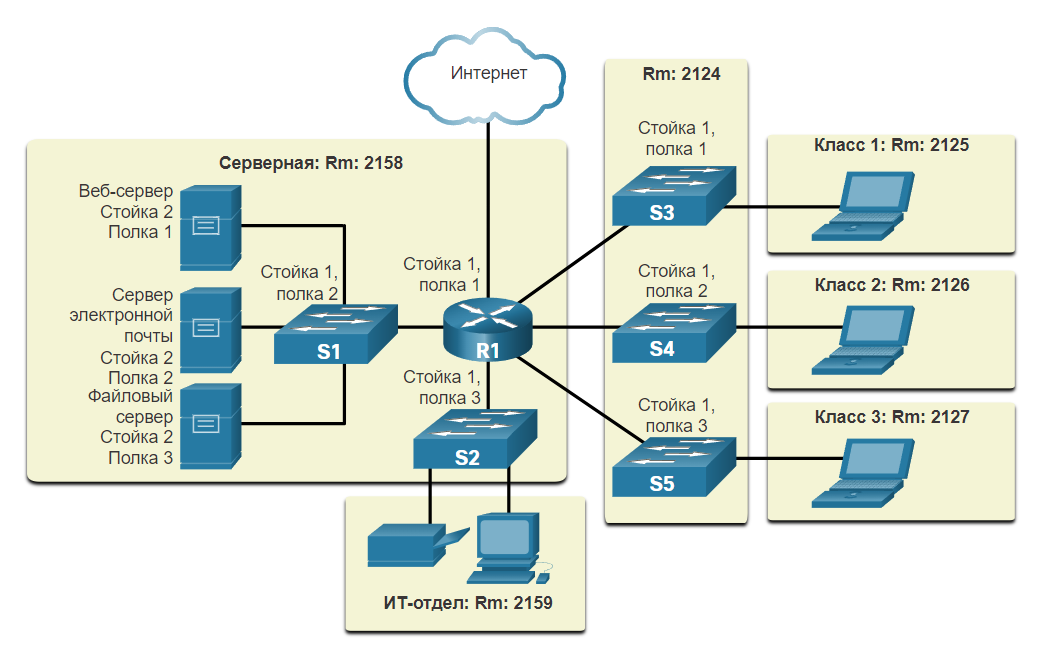
Схемы физической топологии — физическое расположение промежуточных устройств и кабельных линий. Можно видеть, что комнаты, в которых расположены эти устройства, помечены в этой физической топологии.
Топология физической сети показывает шесть комнат, каждая из которых выделена светло-желтым прямоугольником, с различными сетевыми устройствами и кабелями. С левой стороны находится серверная комната с надписью комната 2158. Он содержит маршрутизатор с маркировкой R1, установленный на полке 1 стойки 1 с шестью кабельными соединениями. Кабель в верхней части подключается к облаку с надписью Интернет. Кабель слева подключается к коммутатору с надписью S1, установленному на полке 2 стойки 1. S1 подключен к трем серверам: веб-серверу, установленному на полке 1 стойки 2, почтовому серверу, установленному на полке 2 стойки, и файловому серверу, установленному на полке 3 стойки 2. Кабель, подключенный к нижней части R1, подключается к коммутатору с полотчатой S2 установлен на стойке 1 полка 3. S2 имеет два соединения, ведущие к принтеру и ПК в ИТ-офисе с пометкой комната 2159. R1 имеет три кабеля справа, подключенных к трем коммутаторам, расположенным в комнате 2124. Верхний коммутатор имеет маркировку S3 и установлен на полке 1 стойки 1. Средний коммутатор имеет маркировку S4 и установлен на стойке 1 полке 2. Нижний коммутатор имеет маркировку S5 и установлен на полке 1 стойки 3. S3 имеет кабель слева, подключенный к ноутбуку в комнате, помеченной как класс 1 комната 2125. S4 имеет кабель слева, подключенный к ноутбуку в комнате, помеченной как класс 2, комната 2126. S5 имеет кабель слева, подключенный к ноутбуку в комнате, помеченной как класс 3 комната 2127.
Диаграмма логической топологии
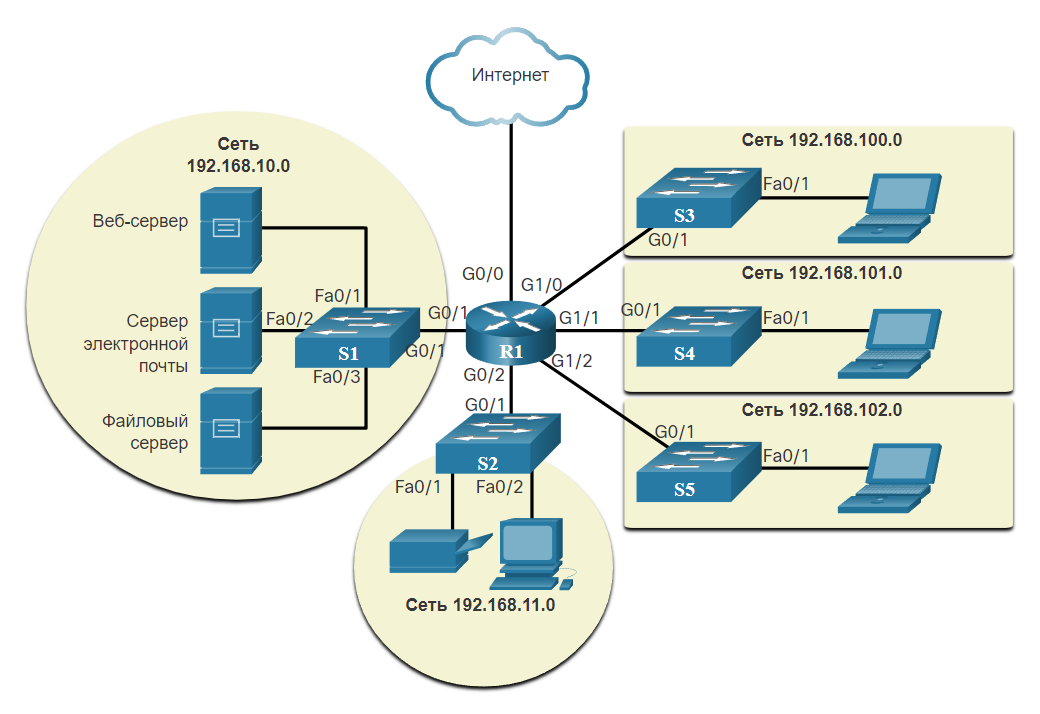
Диаграмма логической топологии иллюстрирует устройства, порты и схему адресации сети, как показано на рисунке. Вы можете увидеть, какие конечные устройства подключены к каким промежуточным устройствам и какие носители используются.
Топология логической сети показывает устройства, метки портов и схему сетевой адресации. В середине изображения находится маршрутизатор с надписью R1. Порт с надписью G0/0 подключается к облаку в верхней части помеченного как Интернет. Порт с надписью G0/1 подключается слева к коммутатору с надписью S1 на порту G0/1. S1 подключен к трем серверам. S1 и серверы выделены светло-желтым кругом с надписью 192.168.10.0 сверху. Порт F0/1 на S1 подключается к веб-серверу. Порт F0/2 на S1 подключается к почтовому серверу. Порт F0/3 на S1 подключается к файловому серверу. Порт F0/1 на R1 подключается внизу к коммутатору с надписью S2. S2 подключается к принтеру и ПК, все из которых выделены в светло-желтый круг с сетью 192.168.11.0, написанной внизу. Слева от R1 расположены три дополнительных соединения, каждое из которых подключается к коммутатору на порту G0/1, который затем подключается к ноутбуку на порту F0/1. Каждый коммутатор и ноутбук выделены желтым цветом и отображается сетевой адрес. Порт G0/0 R1 подключается вверху к коммутатору S3 в сети 192.168.100.0. Порт G1/1 R1 соединяется посередине с коммутатором S4 в сети 192.169.101.0. Порт G1/2 на R1 подключается внизу к коммутатору с надписью S5 в сети 192.168.102.0.
На данном этапе курса вам достаточно знать о топологиях, показанных на схемах физической и логической топологии. Более сложные примеры вы можете найти в Интернете по запросу «схемы сетевой топологии». Если вы добавите слово «Cisco» в поисковую фразу, вы найдете множество топологий с использованием значков, которые похожи на те, что вы видели на этих рисунках.
Теория сети – топология сети
Топология сети – это графическое представление электрических цепей. Это полезно для анализа сложных электрических цепей путем преобразования их в сетевые графы. Топология сети также называется теорией графов .
Основная терминология топологии сети
Теперь давайте поговорим об основной терминологии этой топологии сети.
график
Сетевой граф просто называется графом . Он состоит из набора узлов, соединенных ветвями. В графах узел является общей точкой двух или более ветвей. Иногда только одна ветвь может подключаться к узлу. Ветвь – это отрезок, соединяющий два узла.
Любую электрическую цепь или сеть можно преобразовать в ее эквивалентный график , заменив пассивные элементы и источники напряжения короткими замыканиями, а источники тока – разомкнутыми. Это означает, что линейные сегменты на графике представляют ветви, соответствующие либо пассивным элементам, либо источникам напряжения электрической цепи.
пример
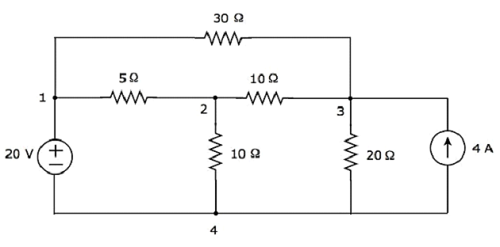
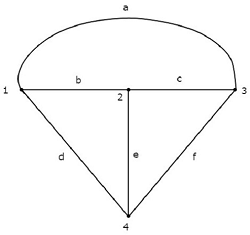
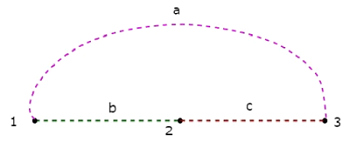
Рассмотрим следующую электрическую цепь .
В вышеупомянутой схеме есть четыре главных узла, и те отмечены как 1, 2, 3 и 4. В вышеупомянутой схеме есть семь ветвей , среди которых одна ветвь содержит источник напряжения 20 В, другая ветвь содержит 4 А Источник тока и остальные пять ответвлений содержат резисторы с сопротивлениями 30 Ом, 5 Ом, 10 Ом, 10 Ом и 20 Ом соответственно.
Эквивалентный график, соответствующий вышеуказанной электрической цепи, показан на следующем рисунке.
На приведенном выше графике есть четыре узла, и они помечены 1, 2, 3 и 4 соответственно. Они такие же, как у основных узлов в электрической цепи. На приведенном выше графике есть шесть ветвей, которые помечены как a, b, c, d, e & f соответственно.
В этом случае на графике мы получили на одну ветвь меньше, потому что источник тока 4 А выполнен в виде разомкнутой цепи, при этом преобразовывая электрическую цепь в эквивалентный график.
Из этого примера мы можем сделать следующие выводы:
- Количество узлов, представленных на графике, будет равно числу главных узлов, присутствующих в электрической цепи.
- Количество ветвей, представленных на графике, будет меньше или равно количеству ветвей, присутствующих в электрической цепи.
Количество узлов, представленных на графике, будет равно числу главных узлов, присутствующих в электрической цепи.
Количество ветвей, представленных на графике, будет меньше или равно количеству ветвей, присутствующих в электрической цепи.
Типы графиков
Ниже приведены типы графиков –
- Связанный график
- Неподключенный график
- Направленный граф
- Ненаправленный граф
Теперь давайте обсудим эти графики один за другим.
Связанный график
Если существует хотя бы одна ветвь между любыми двумя узлами графа, то она называется связным графом . Это означает, что каждый узел в связанном графе будет иметь одну или несколько ветвей, которые связаны с ним. Таким образом, ни один узел не будет представлен как изолированный или разделенный.
График, показанный в предыдущем примере, является связным графом . Здесь все узлы связаны тремя ветвями.
Неподключенный график
Если в графе существует хотя бы один узел, который не связан даже одной ветвью, то он называется несвязанным графом . Таким образом, в несвязном графе будет один или несколько изолированных узлов.
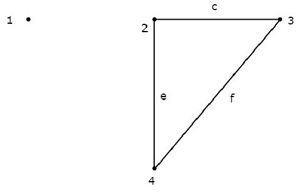
Рассмотрим график, показанный на следующем рисунке.
На этом графике узлы 2, 3 и 4 соединены двумя ветвями каждый. Но ни одна ветвь не была подключена к узлу 1 . Таким образом, узел 1 становится изолированным узлом . Следовательно, приведенный выше граф является несвязным графом .
Направленный граф
Если все ветви графа представлены стрелками, то этот граф называется ориентированным графом . Эти стрелки указывают направление протекания тока в каждой ветви. Следовательно, этот граф также называется ориентированным графом .
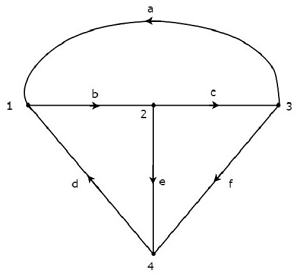
Рассмотрим график, показанный на следующем рисунке.
На приведенном выше графике направление потока тока обозначено стрелкой в каждой ветви. Следовательно, это ориентированный граф .
Ненаправленный граф
Если ветви графа не представлены стрелками, то этот граф называется неориентированным графом . Поскольку нет направления потока тока, этот граф также называется неориентированным графом .
График, показанный в первом примере этой главы, является неориентированным графом , поскольку на ветвях этого графа нет стрелок.
Подграф и его виды
Часть графа называется подграфом . Мы получаем подграфы, удаляя некоторые узлы и / или ветви данного графа. Таким образом, количество ветвей и / или узлов подграфа будет меньше, чем у исходного графа. Отсюда можно сделать вывод, что подграф является подмножеством графа.
Ниже приведены два типа подграфов.
дерево
Дерево является связным подграфом данного графа, который содержит все узлы графа. Но в этом подграфе не должно быть петель. Ветви дерева называются ветками .
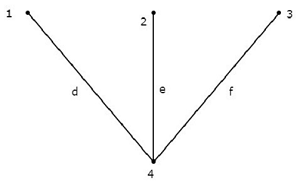
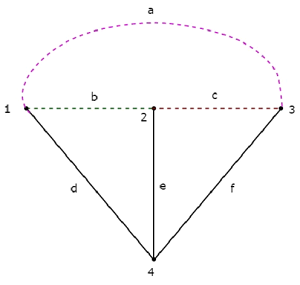
Рассмотрим следующий связанный подграф графа, который показан в Примере начала этой главы.
Этот связанный подграф содержит все четыре узла данного графа и петли нет. Следовательно, это Дерево .
Это дерево имеет только три ветви из шести ветвей данного графа. Потому что, если мы рассмотрим хотя бы одну ветвь из оставшихся ветвей графа, то в вышеуказанном подграфе будет цикл. Тогда результирующий связанный подграф не будет деревом.
Из вышеприведенного дерева мы можем сделать вывод, что количество ветвей , которые присутствуют в дереве, должно быть равно n – 1, где «n» – количество узлов данного графа.
Co-Tree
Co-Tree – это подграф, который состоит из ветвей, которые удаляются при формировании дерева. Следовательно, это называется дополнением дерева. Для каждого дерева будет соответствующее Co-Tree, и его ветви называются ссылками или аккордами. В общем, ссылки представлены пунктирными линиями.
Co-Tree, соответствующее вышеуказанному дереву, показано на следующем рисунке.
Это Co-Tree имеет только три узла вместо четырех узлов данного графа, потому что Узел 4 изолирован от вышеуказанного Co-Tree. Следовательно, Co-Tree не обязательно должен быть связанным подграфом. Это Co-Tree имеет три ветви, и они образуют петлю.
Количество ветвей , присутствующих в совместном дереве, будет равно разнице между количеством ветвей данного графа и количеством веток. Математически это можно записать как
- л количество ссылок.
- b – количество ветвей, присутствующих в данном графике.
- n – количество узлов, присутствующих в данном графе.
Если мы объединим дерево и соответствующее ему Co-дерево, мы получим исходный граф, как показано ниже.
Ветви дерева d, e & f представлены сплошными линиями. Ветви Co-Tree a, b & c представлены пунктирными линиями.