Топология сети передачи данных полный граф это

2. Топология сети передачи данных. Примеры элементарных топологий, основные характеристики. Алгоритмы маршрутизации и методы передачи данных.

1. При организации параллельных вычислений в мультикомпьютерах для организации взаимодействия, синхронизации и взаимоисключения параллельно выполняемых процессов используется передача данных между процессорами вычислительной среды. Временные задержки при передаче данных по линиям связи могут оказаться существенными (по сравнению с быстродействием процессоров) и, как результат, коммуникационная трудоемкость алгоритма оказывает существенное влияние на выбор параллельных способов решения задач.
   1. Примеры топологий сети передачи данных
2. Структура линий коммутации между процессорами вычислительной системы (топология сети передачи данных) определяется, как правило, с учетом возможностей эффективной технической реализации. Немаловажную роль при выборе структуры сети играет и анализ интенсивности информационных потоков при параллельном решении наиболее распространенных вычислительных задач.

Топология сети передачи данных – это структура линий коммутации между процессорами вычислительной системы. Топология представляет собой полный граф, в котором передача данных может быть организована между любыми двумя вершинами (процессорами сети). Топология определяется с учетом возможностей эффективной технической реализации на основе анализа интенсивности передачи информационных потоков. К числу типовых топологий обычно относят следующие схемы коммуникации процессоров (см. рисунок). Полный граф (completely-connected graph or clique) – система, в которой между любой парой процессоров существует прямая линия связи, поэтому данная топология обеспечивает минимальные затраты при передаче данных, однако является сложно реализуемой при большом количестве процессоров. Линейка (linear array or farm) – система, в которой все процессоры перенумерованы по порядку и каждый процессор, кроме первого и последнего, имеет линии связи только с двумя соседними (с предыдущим и последующим) процессорами; такая схема является, с одной стороны, просто реализуемой, а с другой стороны, соответствует структуре передачи данных при решении многих вычислительных задач (например, при организации конвейерных вычислений). 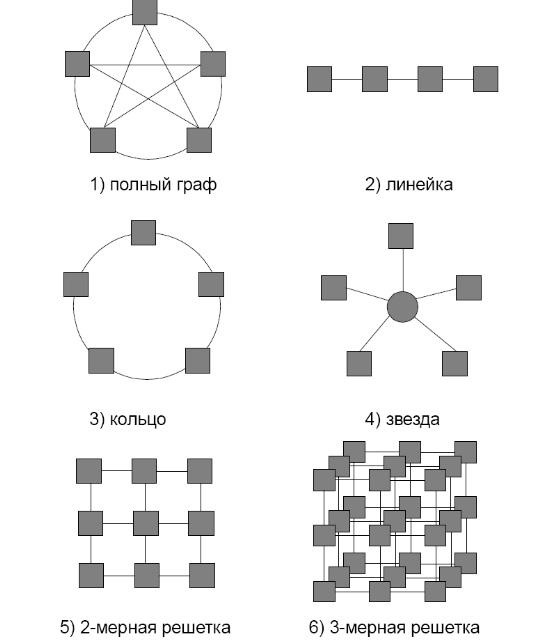Кольцо (ring) – данная топология получается из линейки процессоров соединением первого и последнего процессоров линейки. Звезда (star) – система, в которой все процессоры имеют линии связи с некоторым управляющим процессором; данная топология является эффективной, например, при организации централизованных схем параллельных вычислений. Решетка (mesh) – система, в которой граф линий связи образует прямоугольную сетку (обычно двух — или трехмерную); подобная топология может быть достаточно просто реализована и, кроме того, может быть эффективно использована при параллельном выполнении многих численных алгоритмов (например, при реализации методов анализа математических моделей, описываемых дифференциальными уравнениями в частных производных). Гиперкуб (hypercube) – данная топология представляет частный случай структуры решетки, когда по каждой размерности сетки имеется только два процессора; данный вариант организации сети передачи данных достаточно широко распространен в практике и характеризуется следующим рядом отличительных признаков: а) два процессора имеют соединение, если двоичные представления их номеров имеют только одну различающуюся позицию; б) N-мерный гиперкуб может быть разделен на два (N-1)-мерных гиперкуба (всего возможно N различных разбиений); в) кратчайший путь между любыми двумя процессорами имеет длину, совпадающую с количеством различающихся битовых значений в номерах процессоров (данная величина известна как расстояние Хэмминга). Т.к. каждый процессор может принимать участие только в одной операции приема-передачи данных, то параллельно могут выполняться только те коммуникационные операции, в которых взаимодействующие пары процессоров не пересекаются между собой. Характеристики топологии сети В качестве основных характеристик топологии сети передачи данных наиболее широко используется следующий ряд показателей: • Диаметр – показатель, определяемый как максимальное расстояние между двумя процессорами (под расстоянием обычно понимается величина кратчайшего пути между процессорами); данная величина может характеризовать максимально-необходимое время для передачи данных между процессорами, поскольку время передачи обычно прямо пропорционально длине пути; • Связность (connectivity) – показатель, характеризующий наличие разных маршрутов передачи данных между процессорами сети; конкретный вид данного показателя может быть определен, например, как минимальное количество дуг, которое надо удалить для разделения сети передачи данных на две несвязные области; • Ширина бинарного деления (bisection width) – показатель, определяемый как минимальное количество дуг, которое надо удалить для разделения сети передачи данных на две несвязные области одинакового размера; • Стоимость – показатель, который может быть определен, например, как общее количество линий передачи данных в многопроцессорной вычислительной системе. Алгоритмы маршрутизации Очевидно, что временные задержки при передаче данных по каналам связи при взаимодействии процессов влияют на эффективность параллельных вычислений. Алгоритмы маршрутизации определяют путь передачи данных от процессора-источника до процессора получателя сообщения. Алгоритмы маршрутизации должны определять оптимальный, т.е. кратчайший путь передачи данных с использованием детерминированных и адаптивных методов выбора маршрутов (адаптивные алгоритмы определяют пути передачи данных в зависимости от существующей загрузки коммуникационных каналов). К числу наиболее распространенных оптимальных алгоритмов относится класс методов покоординатной маршрутизации (dimension-ordered routing), в которых поиск путей передачи данных осуществляется поочередно для каждой размерности топологии сети коммуникации. Например, для двумерной решетки такой подход приводит к маршрутизации, при которой передача данных сначала выполняется по одному направлению (например, по горизонтали до достижения вертикали процессоров, в которой располагается процессор назначения), а затем данные передаются вдоль другого направления (данная схема известна под названием алгоритма XY-маршрутизации). Для гиперкуба покоординатная схема маршрутизации может состоять, например, в циклической передаче данных процессору, определяемому первой различающейся битовой позицией в номерах процессоров, на котором сообщение располагается в данный момент времени, и на который сообщение должно быть передано. Время передачи данных между процессорами определяет длительность выполнения параллельного алгоритма в многопроцессорной вычислительной системе. Время передачи данных включает: − время начальной подготовки (t_н) характеризует длительность подготовки сообщения для передачи, поиска маршрута в сети и т.п.; − время передачи служебных данных (t_с) между двумя соседними процессорами (между которыми имеется физический канал передачи данных); к служебным данным может относиться заголовок сообщения, блок данных для обнаружения ошибок передачи и т.п.; − время передачи одного слова данных по одному каналу передачи данных (t_к); длительность подобной передачи определяется пропускной способностью сети. Рассмотрим два наиболее распространенных метода передачи данных. Первый – выполняет передачу сообщений как неделимых (атомарных) блоков информации (store-and-forward routing or SFR). В этом случае процессор-отправитель готовит весь объем данных для передачи, определяет процессор, которому следует направить данные, и запускает операцию передачи данных. Процессор-получатель сообщения, осуществляет прием данных, затем, при необходимости приступает к передаче принятого сообщения далее по маршруту. Время передачи данных t_пд для сообщения размером m байт по маршруту длиной l определяется выражением При достаточно длинных сообщениях временем передачи служебных данных можно пренебречь и выражение может быть записано в более простом виде Второй способ — выполняет передачу сообщений в виде блоков информации, в результате чего передача данных может быть сведена к передаче пакетов. В этом случае принимающий процессор может осуществлять пересылку данных по дальнейшему маршруту непосредственно сразу после приема очередного пакета, не дожидаясь завершения приема данных всего сообщения. Время пересылки данных при использовании метода передачи пакетов будет определяться выражением В большинстве случаев метод передачи пакетов приводит к более быстрой пересылке данных; кроме того, данный подход снижает потребность в памяти для хранения пересылаемых данных для организации приема-передачи сообщений, а для передачи пакетов могут использоваться одновременно разные коммуникационные каналы. С другой стороны, реализация пакетного метода требует разработки более сложного аппаратного и программного обеспечения сети, может увечить накладные расходы (время подготовки и время передачи служебных данных).

Для продолжения скачивания необходимо пройти капчу:

Источник

Примеры топологии сети передачи данных

полный граф (completely- connected graph или clique) – система, в которой между любой парой процессоров существует прямая линия связи. обеспечивает минимальные затраты при передаче данных однако является сложно реализуемой при большом количестве процессоров

Примеры топологии сети передачи данных

линейка (linear array или farm) – система, в которой все процессоры перенумерованы по порядку каждый процессор, кроме первого и последнего, имеет линии связи только с двумя соседними (с предыдущим и последующим) процессорами. просто реализуема соответствует структуре передачи данных при решении многих вычислительных задач (например, при организации конвейерных вычислений)

Примеры топологии сети передачи данных

кольцо (ring) – данная топология получается из линейки процессоров соединением первого и последнего процессоров линейки

Примеры топологии сети передачи данных

звезда (star) – система, в которой все процессоры имеют линии связи с некоторым управляющим процессором. является эффективной, например, при организации централизованных схем параллельных вычислений

Примеры топологии сети передачи данных

решетка (mesh) – система, в которой граф линий связи образует прямоугольную сетку (обычно двух- или трехмерную). может быть достаточно просто реализована эффективна при параллельном выполнении многих численных алгоритмов (например, при реализации методов анализа математических моделей, описываемых дифференциальными уравнениями в частных производных)

Плоская решетка

максимальное расстояние между процессорами равно 6 (количество связей между процессорами, отделяющих самый ближний процессор от самого дальнего) теория показывает, что если в системе максимальное расстояние между процессорами больше 4, то такая система не может работать эффективно при соединении 16 процессоров друг с другом плоская схема является не эффективной.

Примеры топологии сети передачи данных

гиперкуб (hypercube) – данная топология представляет собой частный случай структуры решетки, когда по каждой размерности сетки имеется только два процессора (т.е. гиперкуб содержит 2N процессоров при размерности N).

Гиперкуб

имеет более компактную конфигурацию чем плоская решетка решалась задача о нахождении фигуры, имеющей максимальный объем при минимальной площади поверхности в трехмерном пространстве таким свойством обладает шар. Но, поскольку, нам необходимо построить узловую систему, то вместо шара приходится использовать куб (если число процессоров равно 8) или гиперкуб, если число процессоров больше 8. Размерность гиперкуба будет определяться в зависимости от числа процессоров, которые необходимо соединить. Так, для соединения 16 процессоров потребуется 4-х мерный гиперкуб. Для его построения следует взять обычный 3-х мерный куб, сдвинуть в еще одном направлении и, соединив вершины, получить гиперкуб размером 4

Гиперкуб – отличительные признаки

два процессора имеют соединение, если двоичные представления их номеров имеют только одну различающуюся позицию; в N-мерном гиперкубе каждый процессор связан ровно с N соседями; N-мерный гиперкуб может быть разделен на два (N–1)- мерных гиперкуба (всего возможно N различных таких разбиений); кратчайший путь между двумя любыми процессорами имеет длину, совпадающую с количеством различающихся битовых значений в номерах процессоров (данная величина известна как расстояние Хэмминга) архитектура гиперкуба является второй по эффективности, но самой наглядной

«Толстое дерево» (fat-tree)

Предложена Лейзерсоном (Charles E. Leiserson) в 1985 году. Процессоры локализованы в листьях дерева, в то время как внутренние узлы дерева скомпонованы во внутреннюю сеть. Поддеревья могут общаться между собой, не затрагивая более высоких уровней сети. В настоящее время считается самой эффективной

Источник