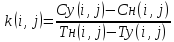Целью оптимизации сетевой модели по ресурсам является

44. Оптимизация сетевых моделей по ресурсам.

С каждой работой, имеющей определенный неизменный объем, связаны затраты на ее выполнение. Как правило, затраты на выполнение работы с неизменным ее объемом возрастают с уменьшением ее продолжительности и снижаются при увеличении ее продолжительности.

В связи с этим возможны варианты организации комплекса работ, отличающиеся продолжительностью его выполнения и затратами на его выполнение.

Для выбора наилучшего варианта служит оптимизация. Оптимальным считается тот вариант, который отвечает заданному критерию.

Оптимизация сетевого графика может осуществляться по следующим двум критериям:

— минимизация времени выполнения комплекса работ при заданных затратах на это выполнение;

— минимизация затрат на выполнение комплекса работ при заданном времени этого выполнения.

Таким образом, нельзя добиться выполнения комплекса работ одновременно в минимальные сроки и с наименьшими затратами.

Целью оптимизации по критерию является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет дополнительных ресурсов, что влечет к повышению затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.

Исходными данными для проведения оптимизации являются:

• нормальная длительность работы;
• ускоренная длительность;
• затраты на выполнение работы в нормальный срок;
• затраты на выполнение работы в ускоренный срок.

45. Оптимизация сетевых моделей по времени и стоимости

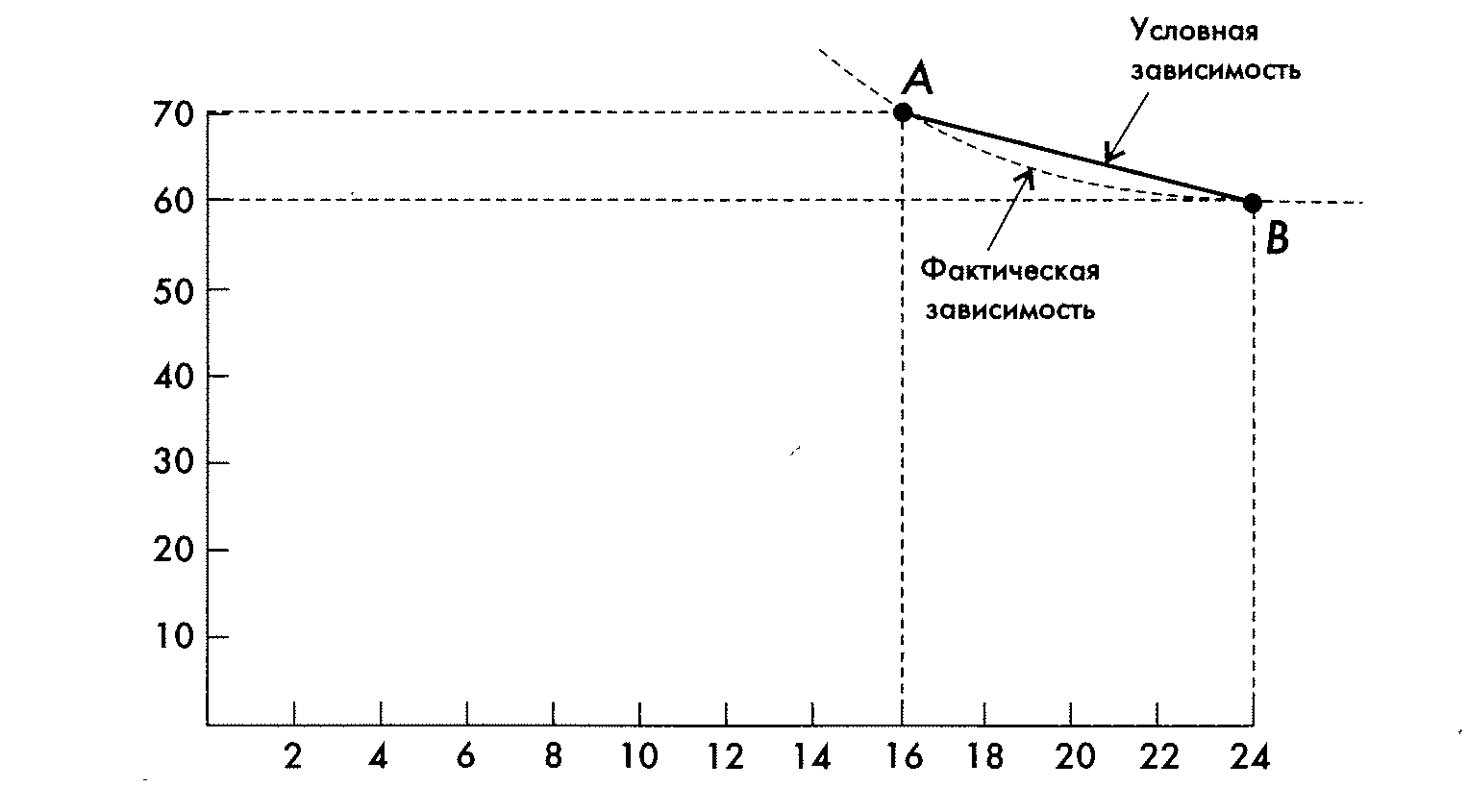
если сокращается продолжительность строитель­ства, то при одновременном снижении накладных расходов прямые рас­ходы возрастают. Функциональная зависимость между продолжительно­стью работ и их стоимостью пока точно не определена. Поэтому рассмот­рим зависимость «время—стоимость» (с учетом прямых затрат), которая может быть определена условно. Как видно из рисунка, точка А соответствует наикратчайшему сроку вы­полнения данного проекта, т.е. сроку, при котором все работы проводятся в предельно сжатые сроки. Точка В соответствует нормальной продолжительности работ. Затраты в точке А, так же как срок, считаются предельными: их дальней­шее увеличение лишь в очень незначительной степени повлияет на сокра­щение сроков. Затраты в точке В являются нормальными. Прямая линия, соединяющая точки А и В, точнее степень наклона этой прямой, и является характеристикой изменения величины прямых затрат при изменении продолжительности работ на единицу времени. Величина наклона для каждой единицы времени является величиной постоянной, так как мы приняли линейную зависимость между продолжительностью и стоимостью работ. (В действительности эта величина является условной. Фактическая зависимость изображена на рис. 7.10 кривой, соединяющей точки А и В.) Величина наклона прямой определяется дробью, в числителе которой — разность между затратами в предельном и нормальном режимах, а в зна­менателе — разность между продолжительностью работ в нормальном и предельном режимах. Для прямой, изображенной на рис. 7.10, эта вели­чина составит: (70 — 60) : (24 — 16) = 1,25 (тыс. руб./день). Для проведения оптимизации необходимо по каждой работе определить предельные и нормальные сроки выполнения, а также предельные и нор­мальные величины затрат. После этого методом последовательного при­ближения достичь заданного предельного срока за счет сокращения про­должительность. 46.Коридорные сетевые графики Коридорный сетевой график представляет собой сетевой график, стрелки (работы) которого расположены в горизонтальных коридорах, соответствующих отдельным исполнителям работ или отдельным комплексам работ. Коридор — горизонтальная зона сетевой модели, объединяющая работы, выполняемые одним исполнителем или относящиеся к одному комплексу (очереди, блоку) Принадлежность работы к тому или иному коридору определяется горизонтальным участком стрелки, обозначающим эту работу. Иногда наглядность коридорного графика можно значительно повысить, показав на нем одновременно и комплексы работ и их исполнителей. Для этого начальные события работ, выполняемых различными исполнителями, изображают в виде различных фигур (кружков, квадратов, треугольников и др.) Коридорный сетевой график несет значительно больше информации, чем обычный сетевой график. Это позволяет использовать коридорные сетевые графики в тех случаях, когда простых сетевых графиков для управленческих функций бывает недостаточно.

Источник

8.3. Оптимизация сетевых моделей

8.3.1. Оптимизация использования ресурса рабочей силы

При оптимизации использования ресурса рабочей силы сетевые работы чаще всего стремятся организовать таким образом, чтобы:

− количество одновременно занятых исполнителей было минимальным;

− выровнять потребность в людских ресурсах на протяжении срока выполнения проекта.

Для проведения подобных видов оптимизации необходим график загрузки.

На графике загрузки по горизонтальной оси откладывается время, например в днях, по вертикальной – количество человек, занятых работой в каждый конкретный день. Для построения графика загрузки необходимо:

− на графике привязки над каждой работой написать количество ее исполнителей;

− подсчитать количество работающих в каждый день исполнителей и отложить на графике загрузки.

Для удобства построения и анализа, графики загрузки и привязки следует располагать один над другим.

Пример построения графика загрузки. Описанные виды оптимизации могут быть выполнены с помощью сдвига работ, который осуществляется за счет резервов времени: свободного или полного. После сдвига работы, работники выполняют ее уже в другие дни, и поэтому для каждого дня изменяется количество исполнителей занятых одновременно.

Резервы работ можно определить без специальных расчетов, только с помощью графика привязки.

Различие в использовании свободных и полных резервов заключается в том, что при сдвиге работы, с использованием свободного резерва, моменты начала следующих за ней работ остаются неизменными (т.е. последующие работы не сдвигаются). При сдвиге работы, с использованием полного резерва, все последующие работы сдвигаются.

8.3.2. Оптимизация типа «время – затраты»

Целью оптимизации по критерию «время – затраты» является сокращение времени выполнения проекта в целом. Эта оптимизация имеет смысл только в том случае, когда длительность выполнения работ может быть уменьшена за счет задействования дополнительных ресурсов, что влечет повышение затрат на выполнение работ. Для оценки величины дополнительных затрат, связанных с ускорением выполнения той или иной работы, используются либо нормативы, либо данные о выполнении аналогичных работ в прошлом.

Исходными данными для проведения оптимизации являются:

− Tн(i,j) – нормальная длительность работы;

− Tу(i,j) – ускоренная длительность;

− Cн(i,j) – затраты на выполнение работы в нормальный срок;

− Cу(i,j) – затраты на выполнение работы в ускоренный срок.

Т.о. каждая работа имеет некоторый максимальный запас времени для сокращения своей длительности Zmax(i,j) =Tн(i,j) −Tу(i,j).

Для анализа сетевой модели в данном виде оптимизации используется коэффициент нарастания затрат (коэффициент ускорения)

который имеет смысл (Дополнительный вопрос: какой смысл?) затрат денежных средств для сокращения длительности выполнения работы (i,j) на один день.

Оптимизация критического пути. Оптимизация критического пути заключается в улучшении его в соответствии с принятым критерием.

В принципе, этими критериями могут быть: время, стоимость, людские и материальные ресурсы и др.

В настоящее время оптимизация сетевых графиков выполняется в основном только по критерию времени.

Оптимизация может производиться с различными целями:

1. если критический путь со временем T превышает заданные сроки T 0, то оптимизация по времени заключается в сокращении критического пути.

Для сокращения критического пути, естественно, имеет смысл форсировать критические работы. Их можно ускорить, например:

1. за счёт дополнительных сил и средств;

2. за счёт переброски сил и средств с некритических работ на критические.

Если используется пункт 1, то возникает типичная задача исследования операций: какие дополнительные средства x 1, x 2 . x n и в какие критические работы нужно вложить, чтобы критический путь T ≤ T 0, а расход дополнительных средств был минимальным.

Если используется пункт 2, т.е. для оптимизации критического пути перебрасываются имеющиеся средства с некритических работ на критические.

Общая схема проведения оптимизации:

1. проводится расчет сети исходя из нормальных длительностей работ;

2. определяется сумма затрат на выполнение всего проекта при нормальной продолжительности работ;

3. рассматривается возможность сокращения продолжительности проекта.

Поскольку этого можно достичь за счет уменьшения продолжительности какой-либо критической работы, то только такие операции подвергаются анализу;

3.1. для сокращения выбирается критическая работа с min коэффициентом нарастания затрат k(i,j), у которой есть запас сокращения времени;

3.2. определяется время Δt(i,j), на которое необходимо сжать длительность работы (i,j). При этом руководствуются следующими соображениями;

3.2.1. максимально возможный запас времени для сокращения работы на текущий момент Z(i,j) ограничивается значением Tу(i,j), т.е.

Z(i,j)=tт(i,j)−Tу(i,j), где tт (i,j) — текущее время выполнения работы

(tт(i,j) =Tн(i,j) только для работ еще не подвергшихся сокращению);

3.2.2. кроме критического пути длительностью Tкр в сети есть подкритический путь длительностью Tп . Критический путь нельзя сократить больше, чем ΔT=Tкр−Tп, поскольку в этом случае критический путь перестанет быть таковым, а подкритический путь наоборот станет критическим;

3.2.3. исходя из вышесказанного, время сокращения длительности выбранной работы (i,j) равно Δt=tт (i,j)−min[Z(i,j),ΔT]. Другими словами, если разность между длительностью критического и подкритического путей ΔT меньше текущего запаса времени сокращения работы Z(i,j), то имеет смысл сокращать работу только на ΔT дней. В противном случае можно сокращать работу полностью на величину Z(i,j);

4. в результате сжатия критической операции получают новый календарный план, возможно с новыми критическими и подкритическими путями, и обязательно с новыми более высокими затратами на выполнение проекта. Это происходит вследствие удорожания ускоренной работы. Общая стоимость проекта увеличивается на ΔC = k(i, j)Δt;

5. переход на шаг 3, который повторяется до тех пор, пока стоимость проекта уменьшается.

В результате оптимизации строится график «Время – затраты».

Под параметрами работ Cн(i,j) и Cу(i,j) понимаются так называемые прямые затраты, т.е. косвенные затраты типа административно-управленческих во внимание не принимаются. Однако их влияние учитывается при выборе окончательного календарного плана проекта. В отличие от прямых затрат косвенные затраты при уменьшении продолжительности проекта убывают, что показано на графике. Оптимальный календарный план соответствует минимуму общих затрат (точка А).

8.3.3. Неопределенность времени выполнения операций

В описанных методах анализа сетей предполагалось, что время выполнения работ точно известно, однако на практике сроки выполнения работ обычно довольно неопределенны. В таких случаях обычно используют экспертные оценки минимальной (a), максимальной (b) и наиболее вероятной длительности (m) работ для расчета их ожидаемой продолжительности.

Данный метод основан на предположении, что время выполнения каждой отдельной работы аппроксимируется β – распределением. При таком подходе можно оценивать вероятности наступления событий в пределах их ранних и поздних сроков, вероятность завершения проекта к заранее установленной дате и другие вероятностные характеристики.

Источник