Практические занятия по сетевым моделям
Сетевое планирование и управление (СПУ) — это графоаналитический метод управления процессами создания (проектирования) любых систем. Сетевой график — полная графическая модель комплекса работ, направленных на выполнение единого задания, в которой (модели) определяются логические взаимосвязи и последовательность работ.
Сетевая модель – это графическое изображение технологической последовательности работ.
Элементы сетевой модели.
Основными элементами сетевого графика являются работа (изображается стрелкой) и событие (изображается кружком).
Работа – это производственный процесс, требующий затрат времени и ресурсов, а также непроизводительного времени. (Работа — это процесс или действие, которые нужно совершить, чтобы перейти от одного события к другому). Если для перехода от одного события к другому не требуется ни затрат времени, ни затрат труда, то взаимная связь таких событий изображается пунктирной стрелкой и называется фиктивной работой. Фиктивная работа представляет собой, таким образом, логическую связь между событиями и показывает зависимость начала выполнения какой-либо работы от результатов выполнения другой.
Фактическая работа в сетевой модели обозначается:
Фиктивная работа:
Событие — это фиксированный момент времени, который представляет собой одновременно окончание предыдущей работы, т. е. ее результат (исключение — начальное событие) и начало последующей работы (исключение — конечное событие).
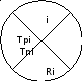
Изображается:
i – индекс (номер) события.
Трi – возможно ранний срок совершения события i;
Раз событие не может произойти, пока не будут выполнены все предшествовавшие ему операции, то ранний срок свершения события определяется наибольшей из всех продолжительностей предшествовавших этому событию путей.
Тпi – допустимо поздний срок совершения события i;
Самое позднее свершение события не должно приводить к увеличению продолжительности критического пути, поэтому поздний срок свершения события определяется разностью между продолжительностью критического пути и наибольшей из всех продолжительностей последующих за этим событием путей.
Ri – резерв времени события.
Любая работа соединяет только два события и отражает процесс перехода от одного события к другому.
Событие, из которого выходит стрелка, называется предшествующим по отношению к данной работе. Событие, в которое стрелка входит, является последующим.
Одно и то же событие (кроме начального и конечного) одновременно является и предшествующим и последующим.
Правила построения сетевых моделей.
- В сетевой модели не должно быть тупиков, т.е. событий, кроме завершающего, из которого не выходило бы ни одной работы.
- В сетевой модели не должно быть событий, кроме исходного, в которое не входило бы ни одной стрелки.
- В сетевой модели не должно быть замкнутых контуров, т.е. путей, соединяющих данное событие с ним же самим. Модель должна быть ориентирована слева направо, необходимо стремиться к отсутствию пересечения работ.
- Каждая работа кодируется шифром двух событий.
Работа i-j – шифр работы, причем j>i i – начальное событие для данной работы; j – конечное событие, результат. Виды путей сетевой модели Путь в сетевой модели представляет собой непрерывную технологическую последовательность работ от исходного события до завершающего. Такой путь называют полным. При этом понятие «путь» распространяется на любую последовательность работ по направлению стрелок. Длина пути определяется суммой продолжительности лежащих на нем работ. Путей в сетевой модели может быть несколько. В отличие от полных путей, имеются еще и укороченные пути, которые отсчитываются от начала модели до данного события (предшествующий путь) или от конца ее до этого же события (последующий путь). В том и в другом случае эти пути представляют собой части полного пути (частичные пути). Сравнением полных путей выявляется такой, суммарная продолжительность работ на котором имеет максимальное значение. Этот путь называется критическим. Он определяет время, необходимое для выполнения программы всех работ, включенных в сетевую модель. Все работы, лежащие на критическом пути, называются критическими, и от их продолжительности зависит конечный срок выполнения программы. Сокращение или увеличение продолжительности критической работы соответственно сокращает или увеличивает общую продолжительность выполнения программы. Кроме того, существует еще подкритический путь. Это тоже полный путь, имеющий продолжительность, близкую с продолжительности критического пути. Ненапряженные пути – это полные пути, продолжительность которых существенно меньше продолжительности критического пути. Характеристики работ сетевой модели.
- Возможно раннее начало работы i-j:
tрнi-j = Трi Поскольку операция не может быть начата, пока не свершится ее начальное событие, то ранний срок начала операции совпадает с ранним сроком свершения ее начального события.
- Возможно раннее окончание работы i-j:
tроi-j = tрнi-j + ti-j
- Допустимо позднее окончание работы i-j
tпоi-j = Tnj
- Допустимо позднее начало работы i-j
tпнi-j = tпоi-j – ti-j Выполнение операции не должно вызывать увеличения продолжительности критического пути, а следовательно, и позднего срока свершения конечного события операции. Так как операция имеет определенную продолжительность, го позднее начало операции вычисляется как разность между поздним сроком свершения ее конечного события и продолжительностью самой операции. Резервы времени работ в сетевой модели. В общем случае работы сетевой модели могут обладать следующими резервами времени:
- полный резерв;
- свободный резерв.
Полный резерв времени у работ, не лежащих на критическом пути, определяется величиной, на которую можно сдвинуть начало данной работы, либо увеличить ее продолжительность, не изменяя при этом конечного срока сетевой модели, т.е. продолжительности ее критического пути. Rпi-j = Тпj – Трi – ti-j Свободный резерв времени у работ, не лежащих на критическом пути, определяется величиной, на которую можно сдвинуть начало данной работы, либо увеличить ее продолжительность, не изменяя при этом ранних сроков начала последующих работ. Rсвi-j = Трj – Трi – ti-j Коэффициент напряженности работ в сетевой модели. На стадии оперативного управления нередко приходиться решать вопрос о целесообразности того или иного перераспределения ресурсов, например, при выбытии из строя оборудования, занятого на критической работе, необходимо принять решение о переключении аналогичного оборудования с другой работы, располагающей резервами времени. При равных резервах у работ следует рассчитывать их коэффициент напряженности. Аналитически: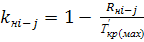 
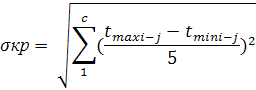
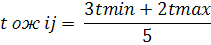
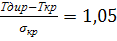
где Т’кр(мах) – продолжительность отрезка критического пути, не совпадающего с максимальным путем, проходящим через данную работу. Вероятностные расчеты сетевого моделирования. После определения критического пути и его продолжительности эту продолжительность сравнивают с установленной продолжительностью работ, называемой директивным сроком – Т дир – обязательным к исполнению. Если такое сравнение дает удовлетворительный результат (Ткр <Тдир), то определяют вероятность совершения конечного события в сроки не позднее Тдир. 
где Ф – функция Лапласа (функция нормального распределения); 
— среднеквадратическое отклонение работ, лежащих на критическом пути от ожидаемого времени Tож. 
tmin ij – оптимистическая оценка времени выполнения работ, т.е. продолжительность выполнения работ при наиболее благоприятных условиях; tmax ij — пессимистическая оценка времени выполнения работ, т.е. продолжительность выполнения работ при наиболее неблагоприятных условиях. 
c – количество работ, лежащих на критическом пути. Если Ркр
→Ткр нов 0,35 0,65 Вероятность выполнения работ в директивные сроки велика. В этом случае вероятней всего должна быть проведена оптимизация сетевой модели по материальным ресурсам, поскольку высокое значение вероятности или, иными словами, малое значение Ткр может быть достигнуто проще всего неоправданно высокими материальными затратами. Если сравнение Ткр>Тдир, то необходима оптимизация модели по времени. 5
Вопрос 23
Какую задачу можно решить методом динамического программирования?
Ответ 1. Задачу о замене оборудования
Ответ 2. Транспортную задачу
Какую особенность имеет динамическое программирование как многошаговый метод оптимизации управления?
Ответ 1. Отсутствие последействия
Ответ 2. Наличие обратной связи
Ответ3. Наличие последействия
Правильным отсечением в задаче целочисленного программирования называется дополнительное ограничение , обладающее свойством
Ответ 1. Оно не должно отсекать найденный оптимальный целочисленный план
Ответ 2. Оно должно быть линейным
Ответ3. Оно должно отсекать хотя бы одно целочисленное решение
Примером задачи целочисленного программирования является…
Ответ 1. Задача о коммивояжере
Ответ 2. Задача линейного программирования
Ответ3. Задача управления запасами
Какой из методов целочисленного программирования является комбинированным…
Ответ3. Метод ветвей и границ
Метод скорейшего спуска является…
Ответ 1. Методом множителей Лагранжа
Ответ 2. Градиентным методом
Ответ3. Методом кусочно-линейной аппроксимации
Множители Лагранжа в экономическом смысле характеризуют…
Ответ 1. Цену (оценку) ресурсов
Ответ 2. Издержки ресурсов
Ответ3. Доход, соответствующий плану
Возможно ли привести матричную игру к задаче линейного программирования
Ответ3. Возможно, если платежная матрица единичная
Верхней ценой парной игры является…
Ответ 1. Гарантированный выигрыш игрока В
Ответ 2. Гарантированный проигрыш игрока В
Ответ3. Гарантированный выигрыш игрока А при любой стратегии игрока В
Платежной матрицей называется матрица, элементами которой являются…
Ответ 1. Выигрыши, соответствующие стратегиям игроков
Ответ 2. Налоговые платежи предприятий
Ответ3. Годовые прибыли отраслевых предприятий
Чистой ценой игры называется…
Ответ 1. Общее значение верхней и нижней ценой игры
Кооперативные игры – это игры…
Ответ 1. Допускающие договоренности игроков
Ответ3. Со смешанными стратегиями
В сетевой модели не должно быть…
Ответ 2. Контуров и петель
Ответ3. Собственных векторов
В сетевой модели не должно быть…
Ответ 2. Тупиковых событий (не имеющих последующих событий), кроме завершающего
Ответ3. Фиктивных работ и тупиковых событий
Математической основой методов сетевого планирования является…
Ответ 1. Теория электрических цепей
Ответ3. Аналитическая геометрия
Критическим путем в сетевом графике называется…
Ответ 1. Самый длинный замкнутый путь
Ответ 2. Самый длинный путь
Ответ3. Самый короткий путь
1.1. Элементы сетевых моделей
1. В каждое событие сети входит не менее одной стрелки (работы кроме исходного события; из каждого события выходит не менее одной стрелки (работы) кроме завершающего события. 2. Все работы должны быть направлены вправо, обратных зависимостей в моделях ПДВ нет. 
Рис. 1.1. 3. В сетевой модели не должно быть «тупиков» и «хвостов». 
хвост тупик Рис. 1.2. 4. Работы не должны иметь одинаковый код. 
неверно верно Рис. 1.3. 5. На сети должно быть как можно меньше пересечений. 
Рис. 1.4. 6. В сети ПДВ не должно быть замкнутых контуров. 
Рис. 1.5. 7. В сетевой модели не должно быть прострелов. 
Рис. 1.6. А – нулевой цикл; Б – возведение надземной части; В – отделочные работы. Нелогичность: отделочники не могут приступить к работе на I (II) здании, пока не возведут фундаменты на II (III) здании. Для правильного отображения связей между работами вводят дополнительный узел. Узел – дополнительное событие, отделяющее начало работы на последующей захватке от окончания работы на данной захватке. 
Рис. 1.7. 8. Правило на исключение лишних событий. Наличие лишних событий ведет к ошибкам в расчете резервов времени работ. Должны выполняться следующие условия: 1) событие действительно, если оно имеет только две стрелки, и при этом имеет смысл: и «конец», и «начало». 
А Б Рис. 1.8. 2) событие действительно, если имеет смысл: только «конец», и только «начало», но при этом должно быть минимум три стрелки. 
Рис. 1.9. Разрабатывая сетевую модель необходимо руководствоваться следующими правилами:
- проверить, какие работы должны быть выполнены до данной;
- проверить, какие работы могут быть выполнены параллельно с данной работой;
- найти работы, которые должны быть выполнены после данной работы.
Для практического закрепления студентами материала выдаются индивидуальные задания, приведенные в приложении 2.
Для продолжения скачивания необходимо пройти капчу: