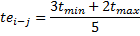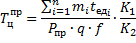В сетевой модели понятие работа это

1. Сетевая модель и ее основные элементы.

Сетевая модель представляет собой план выполнения некоторого комплекса взаимосвязанных работ (операций), заданного в специфической форме сети, графическое изображение которой называется сетевым графиком. Отличительной особенностью сетевой модели является четкое определение всех временных взаимосвязей предстоящих работ.

Главными элементами сетевой модели являются событиями и работы

Термин работа используется в СПУ в широком смысле.Во-первых, это действительная работа — протяженный во временипроцесс, требующий затрат ресурсов (например, сборка изделия, испытание прибора и т.п.). Каждая действительная работа, должна быть конкретной, четко описанной и иметь ответст­венного исполнителя.

Во-вторых, это ожидание — протяженный во времени процесс,не требующий затрат труда (например, процесс сушки после окраски, старения металла, твердения бетона и т.п.).

В-третьих, это зависимость, или фиктивная работа — логическая связь между двумя или несколькими работами (события), не требующими затрат труда, материальных ресурсов или времени. Она указывает, что возможность одной работы непосредственно зависит от результатов другой. Естественно, что продолжительность фиктивной работы принимается равной нулю.

Событие — это момент завершения какого-либо процесса, отражающий отдельный этап выполнения проекта. Событие может являться частным результатом отдельной работы или суммарным результатом нескольких работ. Событие может свершиться только тогда, когда закончатся все работы, ему предшествующие. Последующие работы могут начаться только тогда, когда событие свершится. Отсюда двойственный характер события: для всех непо­средственно предшествующих ему работ оно является конечным, а для всех непосредст­венно следующих за ним — начальным. При этом предполагается, что событие не имеет продолжительности и свершается как бы мгновенно. Поэтому каждое событие, включаемое в сетевую модель, должно быть полно, точно и всесторонне определено, его формулировка должна включать в себя результат всех непосредственно предшествующих ему работ.

Среди событий сетевой модели выделяют исходное и завершающее события. Исходное собы­тие не имеет предшествующих работ и событий, относящихся к представленному в модели комплексу работ. Завершающее событие не имеет последующих работ и событий.

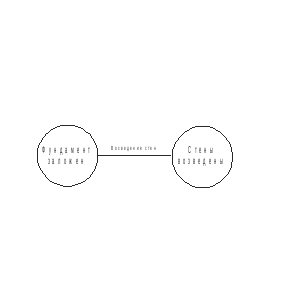
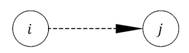
События на сетевом графике (или, как еще говорят, на графе)изображаются кружками (вершинами графа), а работы — стрелками(ориентированными дугами), показывающими связь между работами. Пример фрагмента сетевого графика представлен на рис 1:

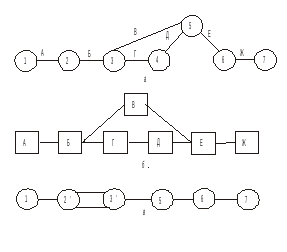
На рис. 2, а приведен сетевой график задачи моделирования и построения оптималь­ного плана некоторого экономического объекта. Чтобы решить эту задачу, необходимо провести следующие работы: А – сформулировать проблему исследования; В5 — матема­тическую модель изучаемого объекта; В — собрать информацию; Г — выбрать метод решения задачи; Д — построить и отладить программу для ЭВМ; Е — рассчитать опти­мальный план; Ж — передать результаты расчета заказчику. Цифрами на графике обозначены номера событий, к которым приводит выполнение соответствующих работ.

Из графика, например, следует, что работы В и Г можно начать выполнять независимо одна от другой только после свершения события 3, т.е. когда выполнены работы А и Б; работу Д — после свершения события 4, когда выполнены работы А, Б и Г; а работу Е можно выполнить только после наступления события 5, т.е. при выполнении всех предшествующих ему работ А, Б, В, Г и Д.

В сетевой модели, представленной на рис. 2 а, нет числовых оценок. Такая сеть называется структурной. Однако на практике чаще всего используются сети, в которых заданы оценки про­должительности работ (указываемые в часах, неделях, декадах, месяцах и т.д. над соответствую­щими стрелками), а также оценки других параметров, например трудоемкости, стоимости и т.п. Именно такие сети мы будем рассматривать в дальнейшем.

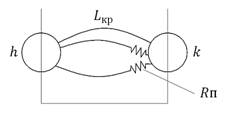
Но прежде сделаем следующее замечание. В рассмотренных примерах сетевые графики со­стояли из работ и событий. Однако может быть и иной принцип построения сетей — без событий. В такой сети вершины графа (например, изображенные прямоугольниками) означают определен­ные работы, а стрелки — зависимости между этими работами, определяющие порядок их выполнения. В качестве примера сетевой график «события — работы» задачи моделирования и построе­ния оптимального плана некоторого экономического объекта, приведенный на рис. 2 а, пред­ставлен в виде сети «работы — связи» на рис. 2 б. А сетевой график «события — работы» той же задачи, но с неудачно составленным перечнем работ, представлен на рис. 2 в (см. правило 3 в разд. 3).

Следует отметить, что сетевой график «работы — связи» в отличие от графика «события — ра­боты» обладает известными преимуществами: не содержит фиктивных работ, имеет более про­стую технику построения и перестройки, включает только хорошо знакомое исполнителям понятие работы без менее привычного понятия события. Вместе с тем сети без событий оказываются значительно более громоздкими, так как событий обычно значительно меньше, чем работ (пока­затель сложности сети, равный отношению числа работ к числу событий, как правило, существенно больше единицы). Поэтому эти сети менее эффективны с точки зрения управления ком­плексом. Этим и объясняется тот факт, что (при отсутствии в целом принципиальных различий между двумя формами пред­ставления сети) в настоящее время наибольшее распространение получили сетевые графики «со­бытия — работы».

Источник

1.2 Основные понятия сетевого планирования

Следует выделить следующие понятия, необходимые для сетевого планирования.

Работа – производственный процесс, требующий затрат времени и материальных ресурсов и приводящий к достижению определенных результатов.

По своей физической природе работы можно рассматривать как действие (например, заливка фундамента бетоном, составление заявки на материалы, изучение конъюнктуры рынка), процесс (пример — старение отливок, выдерживание вина, травление плат) и ожидание (процесс, требующий только затраты времени и не потребляющий никаких ресурсов; является технологическим (твердение цементной стяжки) или организационным (ожидание сухой погоды) перерывом между работами, непосредственно выполняемым друг за другом.

По количеству затрачиваемого времени работа может быть:

• действительной, то есть протяжённым во времени процессом, требующим затрат ресурсов;
• фиктивной (или зависимостью), не требующей затрат времени и представляющей связь между какими-либо работами: передача измененных чертежей от конструкторов к технологам, сдача отчета о технико-экономических показателях работы цеха вышестоящему подразделению.

1.3 Правила построения сетевых моделей

• какие работы должны быть завершены до начала данной работы;
• какие работы должны быть начаты после завершения данной работы;
• какие работы необходимо выполнять одновременно с выполнением данной работы.

Источник

Понятие элемента «работа» сетевой модели.

Работа – это трудовой процесс, требующий затрат времени и ресурсов и соответствующую логическую связь.

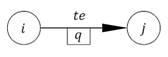
1) «Действительная работа» – требует затраты времени и ресурсов:

– рассматриваемая работа; – время (трудоемкость); – ресурс.

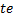
2) «Работа-ожидание» требует только затраты времени:

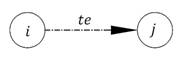
3) Фиктивная работа – устанавливает зависимость и показывает, что выполнение последующих работ находится в прямой зависимости от предшествующей. Не требует ни затрат труда, ни времени.

Виды полных путей сетевой модели.

Полный путь – путь выполнения любых работ от исходного события () до завершающего события ()

1) критический путь – путь максимальной продолжительности от исходного события до завершающего события :

где – трудоемкость рассматриваемой работы.

2) резервные пути – пути, по продолжительности меньше критического:

где – резерв времени.

Определение продолжительности работы стохастической сетевой модели.

где – продолжительность рассматриваемой работы; – наиболее вероятное время выполнения работы; , – минимальное и максимальное время выполнения роботы.

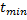
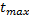
Если в данных нет наиболее вероятного времени, то

Определение продолжительности работы детерминированной сетевой модели.

Для процессов проектирования:

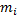
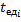
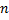
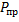
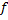
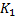
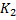
где – объём единицы работ соответствующей номенклатуры (количество технологических карт, чертежей и т.д.); – трудоемкость единицы объема работ соответствующей номенклатуры; – количество номенклатуры в процессе проектирования; – количество исполнителей, рабочих; – продолжительность рабочего дня; – коэффициент календарности (0,84), учитывающий соотношение рабочих и календарных дней в году; – коэффициент, учитывающий время на согласование выполненных работ в процессе проектирования (1,0-1,2); – коэффициент, учитывающий выполнения норм (1,0-1,4).

Для процессов изготовления:

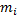
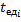
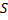
где – объём единицы работ соответствующей номенклатуры в процессе оснастки рабочих мест; – трудоемкость; – мощность цеха подготовки производства по соответствующей номенклатуре оснащения; – количество смен работы цеха; – количество часов работы в смену.

Виды сетевых моделей.

1) Детерминированная модель (метод Ганта);

2) Стохастическая модель (экономико-математическое моделирование сетевого планирования и управления);

3) Сетевая модель в терминах «Событие»;

4) Сетевая модель в терминах «Работа»;

5) Сетевая модель в терминах «Событие-Работа»;

Детерминированная сетевая модель – такая сетевая модель, у которой в основе расчета основной параметр (продолжительность работы) существует в нормативной базе.

Стохастическая сетевая модель – модель неопределенного вида. В условиях вероятностной сетевой модели продолжительность работы определяется на основе вероятностных оценок и закона распределения этих оценок.

СМ в терминах событие – расчетный параметр – событие,а работа – связь между событиями(точка-параметр)

СМ в терминах работа – расчетный параметр – работа, а событие –связь,в виде шифра

Сетевая модель в терминах «Событие-Работа»- определение параметров события и работы (PERT-TIME)

Символика сетевой модели.

События, находящиеся в начале рассматриваемой работы, обозначаются буквой «», а в конце – «». События, стоящие в начале предшествующей работы обозначаются «»(исходное событие), а события в конце последующей работы «» (завершающее событие).

Общий график сетевой модели имеет лишь одно исходное и лишь завершающее событие и фрагменты общего графика сетевой модели, для которых может быть множество начальных и множество конечных событий по отношению к рассматриваемой работе.

Источник