Вероятностная оценка сетевой модели

Вероятностные сетевые модели.

Выше рассматривались постановки задач календарного планирования, не учитывающие вероятностный характер процесса проектирования. Однако во многих случаях при планировании и управлении созданием нового проекта продолжительность работ сетевого графика является случайной величиной, подчиненной некоторому закону распределения. Что касается параметров распределения, то последние задаются для каждой работы их ответственными исполнителями на основе либо нормативных данных, либо априорных соображений, либо своего производственного опыта.

В первых сетевых моделях (РЕRT) для каждой работы задавались три оценки продолжительности выполнения:

— наиболее вероятное время выполнение m;

— оптимистическая оценка времени a;

— пессимистическая оценка времени b.

Наиболее вероятное время определяется как время выполнения работы при нормальных условиях. Оптимистическая и пессимистическая оценки задают размах колебаний продолжительности работы под влиянием неопределенности.

Вероятностная сетевая модель типа РЕRT предполагает, что продолжительность любой работы t есть случайная величина, распределенная по закону бета-распределения на отрезке [а,b] с плотностью

Ожидаемая продолжительность работы приближенно определяется как =(а+4m+b)/6. Среднеквадратическое отклонение от среднего значения  =(b – a)/6.

Вероятностные методы, применяемые в системе PERT.

В системе РЕRT с помощью заданных пользователем трех оценок продолжительности всех работ по вышеприведенным формулам вычисляется средняя продолжительность  и ее дисперсия  2 . Рассматривая среднее значение как фактическую (детерминированную) продолжительность работы, определяют все временные характеристики сети (и критический путь). При этом продолжительность всего проекта определяется как случайная величина, математическое ожидание которой есть сумма средних продолжительностей работ, находящихся на критическом пути, а дисперсия, аналогично, равна сумме всех дисперсий, при допущении, что продолжительности всех работ независимы.

В более общем случае ожидаемое время Mt(i)=M(i) свершения любого i–го события определяется как сумма математических ожиданий времени выполнения работ, лежащих на максимальном пути L между исходным (0) и i–м событиями:

если L=0i₁i₂…i_n= i и Mt(L)  Mt(L), где L любой другой путь между 0 и i–м событиями. Аналогично определяется и дисперсия времени свершения i–м события:

Предполагая выполненными условия центральной предельной теоремы, закон распределения времени окончания проекта (в общем случае, любого события i), считают близким к нормальному, вследствие чего используют интегральную формулу Муавра-Лапласа. Таким образом, оценка p_i вероятности свершения i–го события в запланированный срок t_пл(i) вычисляется по формуле:

где Ф – функция Лапласа (таблица ее значений приведена во всех справочниках по теории вероятности).

Вероятность отсутствия резерва времени для момента окончания работы (i,j) оценивают по формуле:

Двухоценочная методика.

После анализа большого количества сетевых проектов был построен закон распределения продолжительности выполнения работ с плотностью, зависящей лишь от двух параметров [9]:

Это распределение относится к классу бета-распределений и имеет следующие параметры:

— математическое ожидание М(х)=(3а+2b)/5;

— дисперсию D(х)=  2 (х)=0.04(b – а) 2 .

Методика оценки параметров распределения на основании двух задаваемых временных оценок отличается рядом преимуществ по сравнению с трехоценочной методикой системы PERT, прежде всего, за счет уменьшения объема информации, который требуется от исполнителя работы. Эту методику можно с одинаковым успехом применять как при расчете детерминированных (или близких к ним) сетей, так и при моделировании стохастических сетевых проектов.

Рассмотренные нами вероятностные модели и методы определения их временных характеристик использовались большей частью для временного анализа сети и иногда для решения оптимизационных задач типа «время-стоимость».

Основные результаты, получаемые в процессе моделирования вероятностных сетей, следующие:

 получение с определенным уровнем доверительности минимального и максимального времени выполнения проекта;

 получение также с некоторым уровнем уверенности минимального и максимального времени свершения наиболее важных событий;

 оценка вероятности попадания некоторого события на критический путь;

 оценка вероятности попадания работы на критический путь;

 выделение с некоторым уровнем доверительности критического

Источник

IV. Вероятностная оценка времени выполнения работ в сетевом плане

t_ож – математическое ожидание продолжительности работы.

 2 – дисперсия продолжительности работы.

V. Оптимизация сетевой модели.

a) Расчет вероятности наступления завершающего события в заданный срок.

Предполагается, что значение подчиняется закону нормального распределения. Аргумент нормальной функции распределения вероятностей (функции Лапласа — p_{к ()})

где —n число работ, лежащих на критическом пути.

p_к может быть найдена по таблице значений нормальной функции распределения вероятностей в соответствующей справочной литературе.

0,35  p_к  0,65 — вполне достаточны границы допустимого риска;

p_к > 0,65 — на работах критического пути имеются избыточные ресурсы;

Оптимизация сетевой модели в зависимости от полноты решаемых задач может быть разделена на частную и комплексную.

Примеры частной оптимизации:

минимизация времени выполнения проекта при фиксированных затратах;

минимизация численности используемых работников;

минимизация затрат при заданном времени выполнения и др.

Комплексная оптимизация сетевой модели — нахождение оптимального соотношения затрат и сроков выполнения его стадий и этапов.

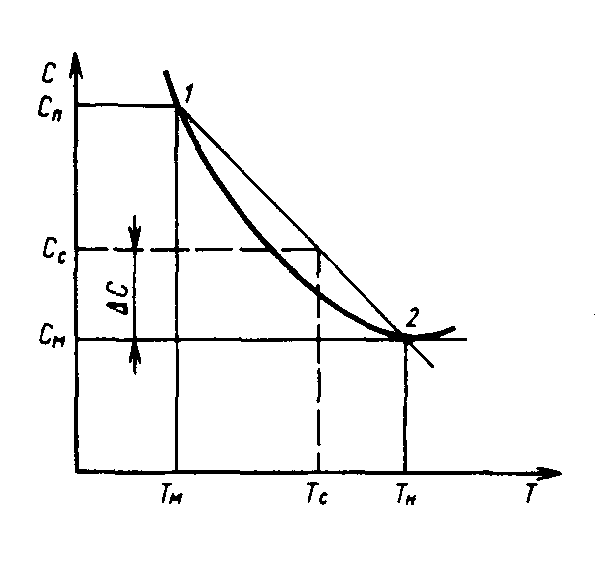
График время — затраты:

Т_м — минимальное время выполнения работы

Т_н — нормальное время (минимальные затраты)

VI. Преимущества спу.

1. Концентрация внимания руководства на решающих работах.
2. В любой момент руководство располагает исчерпывающей информацией.
3. Реализуется принцип непрерывности планирования хода работ и управления ими.
4. Система обеспечивает возможность рационального маневрирования выделенными для данной разработки ресурсами.
5. Устанавливается чёткая взаимосвязь между ответственными исполнителями отдельных работ.

Источник

Сетевые модели с вероятностной оценкой продолжительности работ.

При расчете сетевых моделей методом PERT продолжительность работ является случайной величиной, подчиняющейся собственному закону распределения, а значит, обладающей собственными числовыми характеристиками. Такими характеристиками являются средняя продолжительность работы (t ср ) и дисперсия оценки продолжительности работы ( 2 ).

Исходными данными для расчетов служат экспертные оценки продолжительностей работ:

• t о — оптимистическая оценка, т.е. оценка продолжительности работы при благоприятных условиях;
• t п — пессимистическая оценка, т.е. оценка продолжительности работы при неблагоприятных условиях;
• t нв — наиболее вероятностная оценка, т.е. оценка продолжительности работы при нормальных условиях;

Вероятностные характеристики продолжительности отдельных работ используются для определения параметров всего проекта в целом. Когда средняя продолжительность каждой работы определена, продолжительность (и прочие показатели) проекта в целом рассчитываются с помощью уже известных алгоритмов, только при этом в качестве продолжительности работ используется средняя продолжительность. Значения всех аналитических параметров сетевого графика – длины критического пути, определяющего продолжительность всего проекта, и ранних и поздних наступлений событий, резервов событий и работ – будут такими же, как если бы мы использовали не среднюю, а обыкновенную продолжительность работ.

Обобщенной вероятностной оценкой продолжительности всего проекта является средняя длина критического пути сетевого графика, которая вычисляется как сумма всех средних продолжительностей работ, лежащих на критическом пути.

Дисперсия является мерой диапазона возможных значений продолжительности, или мерой разброса оценок. Если дисперсия велика, это значит, что и неопределенность продолжительности выполнения работ велика. Иными словами, различные значения продолжительности имеют почти равную вероятность. Если дисперсия мала, это означает, что неопределенность продолжительности выполнения работы мала, т.е. время выполнения работы определено более или менее точно.

Работа, не лежащая на критическом пути, но обладающая большей дисперсией, чем критическая работа, может превратиться в критическую работу и существенно изменить весь сетевой график проекта.

Календарный план: содержание, назначение, элементы, алгоритм построения.

Календарное планирование в управлении проектами – это ключевой и важный процесс, результатом которого является утвержденный руководством компании календарный план проекта (часто его называют еще планом-графиком, календарным графиком, планом управления проектом). Цель календарного планирования – получить точное и полное расписание проекта с учетом работ, их длительностей, необходимых ресурсов, которое служит основой для исполнения проекта.

Календарное планирование включает в себя:

планирование содержания (scope) проекта и построение СДР — структурной декомпозиции работ, или WBS (Work Breakdown Structure);

определение последовательности работ и построение сетевого графика;

планирование сроков, длительностей и логических связей работ и построение диаграммы Ганта;

определение потребности в ресурсах (люди, машины и механизмы, материалы и т.д.) и составление ресурсного плана проекта;

расчет затрат и трудозатрат по проекту.

Составление календарного плана-графика проекта включает в себя несколько аспектов. Мы должны спланировать сроки и длительности работ, определить их последовательность и взаимосвязи, подумать о необходимых ресурсах, учесть стоимость этих работ и ресурсов.

Следующий шаг по созданию календарного плана проекта – это определение длительностей работ и их взаимосвязей. Например, какие-то работы в нашем списке могут выполняться строго последовательно, а какие-то – параллельно друг с другом во времени. Для того чтобы «увязать» сроки работ по проекту, их продолжительность и зависимости, сегодня во всем мире менеджеры проектов используют простой и вместе с тем полезный инструмент календарного планирования – диаграмму Ганта (иногда пишется «диаграмма Гантта»). Диаграмма Ганта – это наглядное представление календарного плана-графика проекта, в котором слева расположен иерархический перечень всех работ проекта (СДР), и справа – календарь с конкретными датами. Работы обозначены полосками, связи между работами — стрелками.

Источник