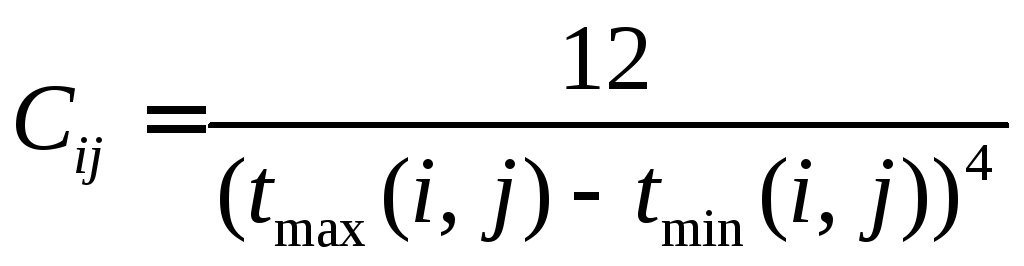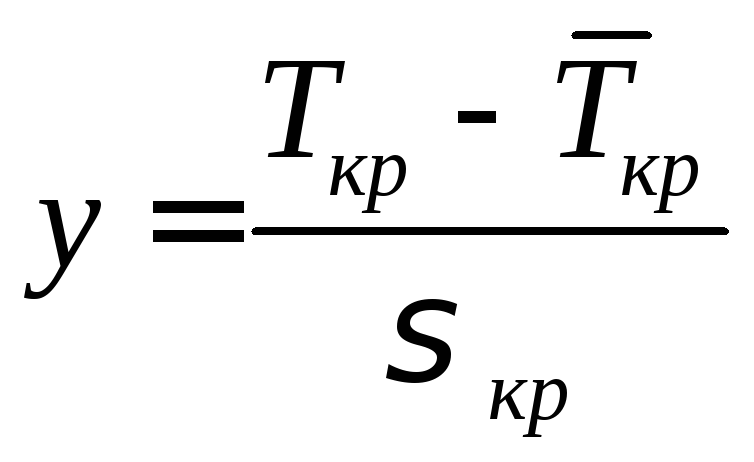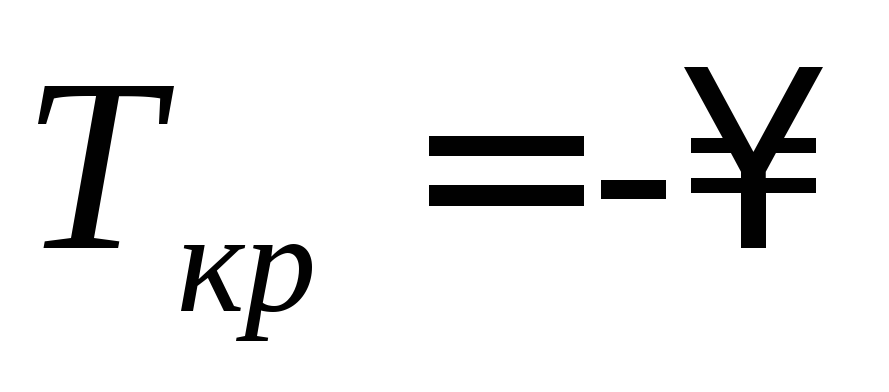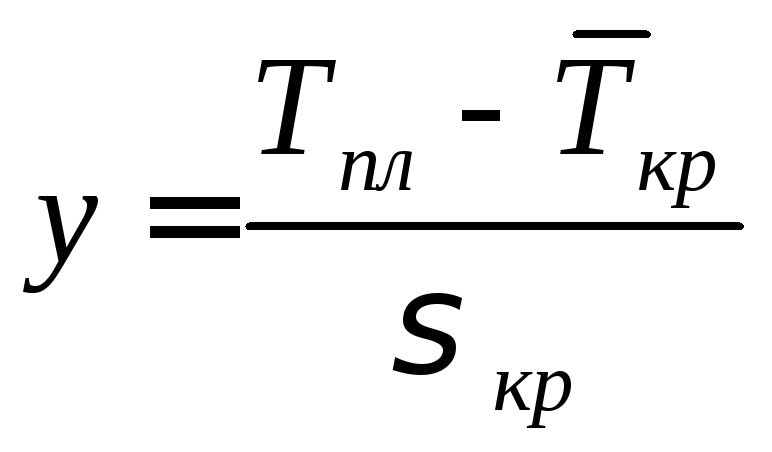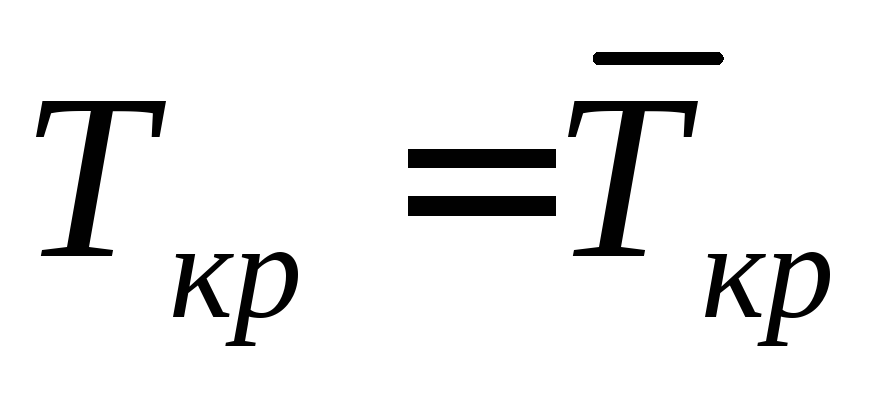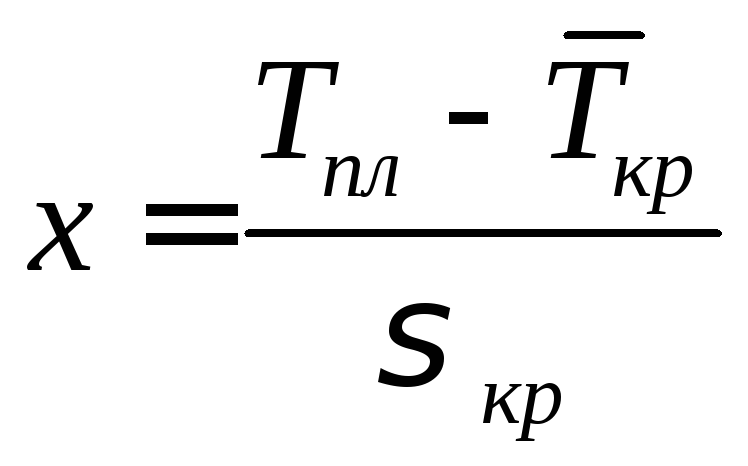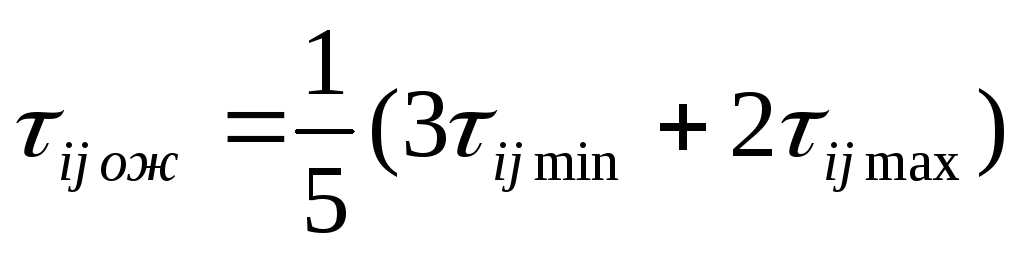Вероятностные параметры сетевой модели

Вероятностная сетевая модель

В реальной дейст­ви­те­ль­ности имеет место неопределенность как в структуре гра­фа (те или иные события или работы могут при­сутствовать или же нет), так и во временных параметрах — времена выполнения работ, моменты на­сту­п­ления событий, резервы и пр. Одним из распространенных методов расчета является метод PERT , использующий ряд упрощающих предположений по сравнению с общей постанов­кой задачи ра­счета вероятностных сетей:

Предполагается, что времена работ t(i,j) подчиняются β-распределению, в котором параметры α_ij и γ_ij одинаковы для всех работ, причем

α_ij =α =1

γ_ij =γ=2

Тогда функция распре­деле­ния длительности работы (i,j) принимает вид:

Для таких распределений в качестве приближенных значений для моментов могут быть приняты следующие оценки

Математическое ожидание:

Предполагается статистическая независимость длительностей работ.

Предполагается, что длительность критического пути настолько пре­во­с­хо­дит (в среднем) дли­те­ль­ности прочих полных путей, что практически невоз­мо­жен его случайный «перескок» на другие пути.

Порядок расчета вероятностной модели методом pert

После того, как осуществлена нумерация вершин и собраны данные по t_max и t_min проводятся следующие расчеты.

Для всех работ собираются данные по tmax и tmin;

Определяются моменты распределений длительностей работ tож(i,j), ;

На основании совокупности значений t(i,j) = tож(i,j) проводится обыч­ный расчет характеристик, как для детерминированной сетевой модели;

Определяется критический путь Lкр и его среднее значение

Определяется дисперсия длительностей Lкр как сумма дисперсий дли­те­ль­но­­стей критических ра­бот (предположение о независимости работ)

Поскольку длительности t(i,j) – независимые случайные величины, их сумма Tкр может тракто­ваться как случайная величина, распре­де­лен­ная по нор­ма­ль­но­му законус матожи­да­ни­еми дис­пер­си­­ей, для ко­то­ро­го фу­н­кция плотности вероятности имеет вид:

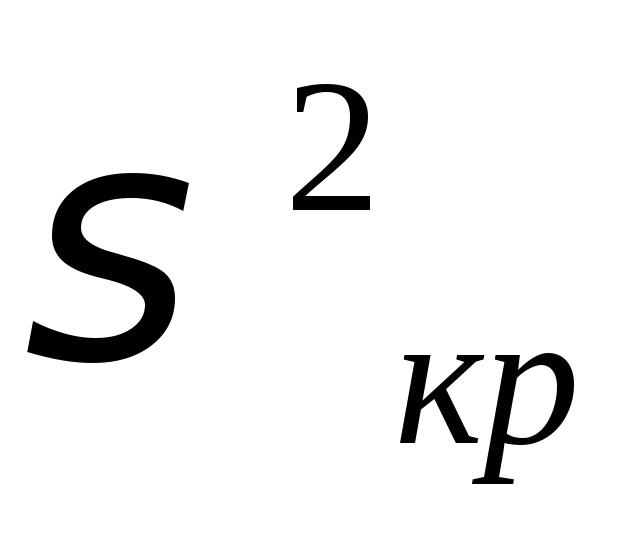
Поскольку из свойств нормального распределения следует (правило «трех си­гма»), что с вероят­но­с­тью 0,9974 значение Ткр будет нахо­ди­ть­ся в интервале

,

,

Пусть определен некоторый плановый срок выполнения всего проекта – Тпл.

Вероят­ность P (Tкр ≤ Tпл) выполнения работы в срок определяется сле­ду­ю­щим образом:

Для того, чтобы получить конкретные значения для этой функции, не­об­хо­ди­­мо перейти от 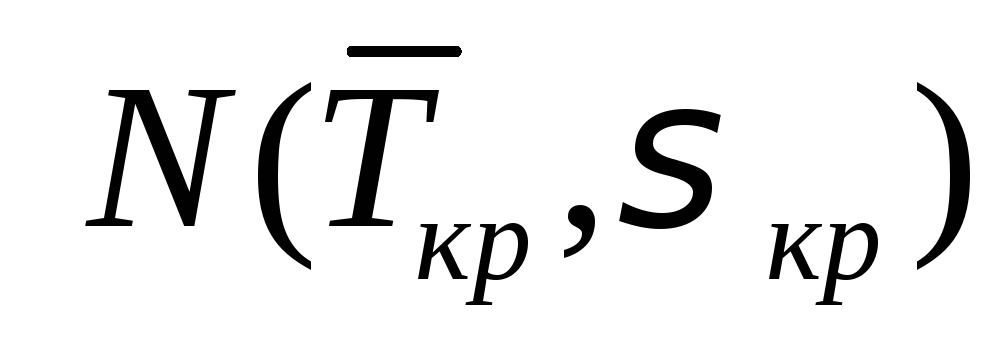к ста­ндартному табулированному ра­спре­де­ле­­нию . С этой целью осуществляется замена переменной:

что приводит к изменению подинтегральной функции и пределов интегрирования:

где Ф(х) называется функцией Лапласа и табулирована. Значение ее мо­ж­но та­к­­же получить с ис­по­льзованием библиотечных функций, ко­то­рые при­­сут­ствуют во многих компиляторах и про­г­рам­м­ных пакетах. В час­т­но­сти, в таб­ли­чном процессоре Microsoft Excel она представлена функцией нормстрасп().

Источник

Расчет и исследование сетевой модели

Расчет сетевой модели заключается в определении

• критического времени и критического пути;
• полных, независимых и частных резервов времени работ;
• резервов времени событий.

Удобно исследование сетевой модели изображать линейной диаграммой (графиком Ганта), в которой каждая работа – отрезок, параллельный оси времени. Длина этого отрезка равна продолжительности работы в выбранном масштабе. События i и j начала и конца работы u_ij ставят в начале и конце соответствующего отрезка. Отрезки располагают один над другим, снизу вверх, в порядке возрастания индексации. Момент наступления исходного события равен 0. Каждый отрезок (i,j) размещают на диаграмме таким образом, чтобы его начало совпало с самым правым концом всех отрезков, входящих в событие i. На рис. 2.11 представлена линейная диаграмма сетевого графика, изображенного на рис. 2.10. 24 5 Н 3 5 3 4 2 5 1 3 0 3 0 2 10 1 0 1 2 3 4 5 10 t Рис. 2.11 Линейная диаграмма сетевой модели Не трудно заметить, что исходная линейная диаграмма отражает такой ход ведения работ, при котором все работы начинаются в свои ранние сроки. С помощью линейной диаграммы можно определить критический путь, критическое время, резервы времени всех работ и т.д. Критический путь представляет собой цепочку отрезков-работ, соединяющих завершающее событие самого правого отрезка с исходным. Критическое время равно самой правой координате всех отрезков линейной диаграммы. Полный резерв времени работы равен максимальному сдвигу соответствующего отрезка вправо, который при этом не приведет к увеличению критического времени. Так, P_п(4,5) = 6, P_п(1,3) = 6. На диаграмме символами н, 1, 2 обозначены работы, имеющие соответственно независимый и частные резервы 1-го и 2-го вида. Жирной рамкой выделены критические работы. После расчета сетевой модели переходят к ее исследованию, целью которого является получение такого графика выполнения работ, который наиболее полно удовлетворяет каким-то критериям. Для этого можно увеличивать длительность или задерживать начало выполнения работ, во-первых, на величину их независимых резервов, что не требует пересчета резервов других работ, во-вторых, на величину их свободного резерва (т.е. частного резерва 2-го вида), так как это не влечет за собой пересчет резервов последующих работ и т.д. Тем самым от исходной переходят к другим линейным диаграммам, в которых работы могут либо начинаться не в свои ранние сроки, либо выполняться более начальной продолжительности, однако при этом срок завершения всего комплекса работ не меняется, оставаясь равным критическому.

Лекция 2.3.3. Более сложные сетевые модели

Вероятностная временная сетевая модель

Второй также наиболее часто встречающейся сетевой моделью является одноцелевая временная вероятностная модель. Эта модель отличается тем, что продолжительности работ задаются как случайные величины. Такая модель более близка к условиям подсистемы ТПП. В настоящее время существуют две методики задания параметров распределения продолжительности работ:

• трехоценочная;
• двухоценочная.

При использовании первой методики эксперт задает 3 оценки продолжительности работы:

• оптимистическую τ_ijmin;
• наиболее вероятную τ_ijнв;
• пессимистическую τ_ijmax.

Наиболее вероятная оценка – это время, необходимое для выполнения данной работы при нормальных, чаще всего встречающихся условиях (определяется первой). Оптимистическая оценка – это время, необходимое для выполнения работы при наиболее благоприятном стечении обстоятельств (определяется второй). Пессимистическая оценка – это время, необходимое для выполнения работ при неблагоприятных условиях. Как вы знаете, продолжительность работы связана с количеством ресурсов, выделяемых на ее проведение. Поэтому необходимо отметить, что для определения временных характеристик продолжительности работы эксперты должны руководствоваться максимальными значениями ресурсов. При использовании второй методики исключается наиболее вероятная оценка τ_ijнв, определение которой вызывает у экспертов особые трудности и пользуются только двумя оценками τ_ijmin и τ_ijmax. На основе опытных данных установлено, что в большинстве случаев законы распределения продолжительностей работ обладают положительной асимметрией, распределение более круто в области τ_ijmin. Это позволило из множества теоретических законов распределения выбрать закон β-распределения, кривая плотности которого имеет вид, представленный на рис.2.12. При этом оценки математического ожидания и дисперсии β-распределения определяются следующим образом: P(t) мода t_ijож t_ijt_ijmin t_ijнв t_ijmax Рис. 2.12 Вид плотности распределения продолжительности работ По второй методике: Первый этап расчета временной вероятности модели заключается в определении:

1. ожидаемого времени выполнения работ τ_ijож и оценки дисперсии σ 2 _ij.
2. всех временных параметров модели по тем же алгоритмам, что и у детерминированной временной модели, заменив τ_ij на τ_ijож.

Второй этап расчета заключается в определении вероятности наступления каждого события сети не позднее директивных сроков. Обозначим через μ_i – случайную величину, характеризующую ранний срок наступления события i. Если событие i связано с исходным событием лишь одним путем L(0i), то оценка математического ожидания μ_iопределяется суммой ожидаемых продолжительностей работ, принадлежащих этому пути t_ож[L(0i)], а оценка дисперсии σ 2 (μ_i) представляет собой сумму дисперсий продолжительностей тех же работ. В случае, если имеется более одного пути, предшествующего i-му событию, то упрощенно предполагается, что в этом случае μ_i и σ 2 (μ_i) вычисляется с использованием характеристик предшествующего пути, имеющего максимальную продолжительность max t[L(0i)]. Если же несколько путей имеют максимальную продолжительность, то для определения дисперсии выбирается путь с максимальной дисперсией продолжительности, так как он характеризуется большой неопределенностью, а, следовательно, дает более надежный результат. Таким образом, где k означает работы, принадлежащие самому длинному пути, предшествующему событию i. При этом предполагается, что величина μ_i является суммой независимых случайных величин, и, следовательно, согласно центральной предельной теореме, распределение μ_i близко к нормальному, а величины (*) являются оценками математического ожидания и дисперсии. Поскольку μ_i есть ранний срок наступления события i, то это событие наступит не позднее директивного срока T_Дi с вероятностью P( μ_i ≤ T_Дi ). Переходя к стандартному нормальному распределению величины получим Здесь Ф – стандартное (нормированное) нормальное распределение величиныx_i, K_i – квантиль данного распределения. Обычно в качестве директивных сроков всех событий кроме завершающего используют поздний срок его свершения T_i п . Для завершающего события величина T_Д определяется лицом, принимающим решение, причем T_n P _ож = t_кр.

Источник

7.17. Вероятностные сетевые модели

Вероятностные модели — это такие модели, отдельные характеристики которых являются случайными величинами. Среди них выделяют модели с неопределенностью продолжительности работ.

Продолжительность каждой работы такой сетевой модели задастся функцией распре делении её случайной продолжительности

Представленный график функции имеющий вид функции распределения», иллюстрирует свойства случайной продолжительности : возможные значения лежат между (оптимистическая оценка продолжительности) и — (пессимистическая оценка продолжительности).

Существует наиболее вероятное значение при котором плотность распределения достигает максимума.

Значения задаются проектировщиками. Соответствующее среднее значение возможной продолжительности рассматри­ваемой ра6оты определяется по формуле:

а дисперсия се продолжительности

Такой метод оценки продолжительности работ очень прост. Бо­лее того, он сводит расчёт сложных вероятностных моделей к методи­ке расчета детерминированных сетевых моделей, которые мы рас­смотрели выше.

Вопросы для самопроверки

1. Что следует понимать под моделированием строительного производства?
2. Что представляют собой линейные графические модели строительного производства? Их преимущества и недостатки?
3. Что следует понимать под сетевой моделью строительного производства?
4. Какие основные элементы сетевых моделей строительного производства?
5. Как изображаются в сетевых моделях последовательность ра­бот при последовательном, параллельном и лоточном методах организации работ?
6. Какие правила построения сетевых моделей необходимо выполнять при разработке сетевых моделей организации работ?
7. Какие временные параметры сетевых моделей вы знаете?
8. Как осуществляется кодирование работ сетевых молелей?
9. Что необходимо понимать под ранним началом и ранним окончанием работ?
10. Что необходимо понимать под поздним началом и поздним окончанием работ?
11. Что следует понимать под общим и частным резервами времени работ?
12. В чём суть методики расчета сетевых моделей табличным методом?
13. В чём суть методики расчёта сетевых моделей непосредственно па графике?
14. Что называется потенциалом события, и как рассчитываются сетевые модели по потенциалам событий?
15. Какие особенности расчёта сетевых моделей с использованием ЭВМ?
16. Как построить сетевую модель организации выполнения работ в масштабе времени?
17. Что значит корректировка сетевых графиков по времени выполнения работ и как корректируются сетевые графики за счёт перераспределения трудовых ресурсов?
18. Как корректируются сетевые графики по времени выполнения работ за счёт совмещения технологических процессов и при­влечения дополнительных трудовых ресурсов?
19. Что значит преобразование сетевого графика в линейный и как выполняется этот процесс?
20. Цель и методика корректировки сетевых графиков по использованию ресурсов?
21. Цель и методика корректировки сетевые графиков с учетом стоимости работ?
22. Какая последовательность разработки и этапы Применения сетевых графиков?
23. Что понимается под вероятностными сетевыми моделями, и как определяются продолжительности работ с учётом вероятности продолжительности их выполнения?

Источник