Параметры сетевых моделей и методы их расчета
Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события tр(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
tр(i) = max t[Lр(i)] (2.1)
Например, tр(7)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17 < t(L2)=7+12=19.
Ранний срок начала работы tр.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
tр.н.(i,j)=max t[Ln(i)](2.2)
Например, tр.н.(7,11)=19, т.к. L1=(1,2,4,7), L2=(1,3,4,7),
t(L1)=5+12=17
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
tр.н.(i,j) = tр(i) (2.3)
Ранний срок окончания работы tр.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
tр.о.(i,j)= tр.н.(i,j) + t(i,j) (2.4)
Например, tр.о.(7,11)= tр.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события tп( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
tп(i) =Tкр — max t[Lк(i)](2.5)
Например, tп(7)=19, т.к. L1=(7,11), L2=(7,9,11), t(L1)=8 > t(L2)=4,
tп(7) = Tкр — max t[Lк(7)]=27 — 8=19.
Для событий критического пути tр( i)=tп(i), для других событий tр(i)tп(i).
Поздний срок окончания работы tп.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
tп.о.(i,j)=Tкр — max t[Lк(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события tп.о.(i,j) = tп(j). Например, tп.о.(4,7) = tп(7)=19.
Поздний срок начала работы tп.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
tп.н.(i,j)= tп .о.(i,j) — t(i,j) (2.7)
Например, tп.н.(4,7)= tп.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: tр.н.(4,7)= tп.н.(4,7)=7, tр.о.(4,7)= tп.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени Rп( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
Rп (i,j)= tп(j) — tр(i) — t(i,j)
Rп(i,j)= tп.н (i,j) — tр.н.(i,j) (2.8)
Rп (i,j)= tп.о.(i,j) — tр.о.(i,j)
Свободный резерв времени Rс( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
Rс(i,j)= tр.н (j,к) — tр.о.(i,j) (2.9) Перейти к онлайн решению своей задачи
Методы расчета временных параметров и критического пути сетевой модели проекта
Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.
Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.
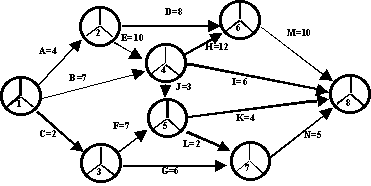
В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.
Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров
Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая – индексу конечного события работы. С учетом этого замечания:
- Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е. ESTij = EET [i].
- Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е. LFTij = LET [j].
- Раннее время окончания работы [ij]: EFTij = ESTij + tij.
- Позднее время начала работы [ij]: LSTij = LFTij – tij.
- Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е. EET[j] = max , где [rj], [nj], . [mj] – индексы работ, для которых событие [j] является конечным.
- Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е. LET[j] = min < LSTjr, LSTjn, . LSTjm>, где [jr], [jn], . [jm] – индексы работ, для которых событие [j] является начальным.
- Для исходного и заключительного события сетевой модели справедливо: EET[s] = LET[s]
- Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо: EET[f] = LET[f] = TK, где TK – продолжительность критического пути.
- Полный резерв времени выполнения работы [ij]: TFij = LЕT[j] – EET[i] – tij.
- Свободный резерв времени выполнения работы [ij]: FFij = EЕT[j] – EET[i] – tij.
- Независимый резерв времени выполнения работы [i]: IFi = EЕT[j] – LET[i] – tij.
Методы расчета временных параметров и критического пути сетевой модели проекта
Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.
Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.
В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.
Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров
Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая – индексу конечного события работы. С учетом этого замечания:
- Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е. ESTij = EET [i].
- Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е. LFTij = LET [j].
- Раннее время окончания работы [ij]:
- Позднее время начала работы [ij]: LSTij = LFTij – tij.
- Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е. EET[j] = max , где [rj], [nj], . [mj] – индексы работ, для которых событие [j] является конечным.
- Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е. LET[j] = min < LSTjr, LSTjn, . LSTjm>, где [jr], [jn], . [jm] – индексы работ, для которых событие [j] является начальным.
- Для исходного и заключительного события сетевой модели справедливо: EET[s] = LET[s]
- Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо: EET[f] = LET[f] = TK, где TK – продолжительность критического пути.
- Полный резерв времени выполнения работы [ij]: TFij = LЕT[j] – EET[i] – tij.
- Свободный резерв времени выполнения работы [ij]: FFij = EЕT[j] – EET[i] – tij.
- Независимый резерв времени выполнения работы [i]: IFi = EЕT[j] – LET[i] – tij.
4,Основные временные параметры сетевых моделей
Расчет сетевой модели заключается в определении следующих временных расчетных параметров отдельных составляющих ее работ: 1. Ткр — продолжительность критического пути – максимальная продол-жительность выполнения всех работ, что в конечном итоге определяет сроки строительства; 2. Ri-j – общий (полный) резерв времени работы i-j – максимальное время, на ко-торое можно увеличить продолжительность выполнения работы i-j, или перенести сроки ее начала на более позднее не изменяя при этом продолжительность критического пути; 
3. ri-j – частный (свободный) резерв времени – максимальное время, на которое можно увеличить продолжительность выполнения работы i-j, или перенести сроки ее начала на более позднее не изменяя при этом ранних начал последующих работ; 
4. ti-j – продолжит-ть выполнения работы i-j; 5. ti-jрн – время раннего начала работы i-j – самый ранний срок возможного начала работы i-j; 6. ti-jро – время раннего окончания работы i-j – самый ранний срок воз-можного окончание работы i-j; 7. ti-jпн – время позднего начала работы i-j – самый поздний срок возмож-ного начала работы i-j; 8. ti-jпо – время позднего окончания работы i-j – самый поздний срок окон-чания работы i-j; Существуют различные методы расчета временных параметров сетевых моделей: -графический (секторный, или на самом графике) -аналитический -табличный -метод потенциалов -метод дроби Расчет можно выполнять как вручную, так и помощью ЭВМ.
5. Исходные данные по разработке пос.
- Технико-экономическое обоснование или технико-экономические расчеты, обосновывающие хозяйственную их необходимость и экономическую целесообразность строительства данного объекта и задания на его проектирование.
- Материалы инженерных изысканий.
- Плановые документы, устанавливающие сроки строительства.
- Согласованные генподрядными и субподрядными организациями решения по применению материалов, конструкций, средств механизации, порядка обеспечения мест строительства водой, врем. инженерными сетями.
- Сведения обусл. поставки и транспортирования с предприятий-поставщиков строительных конструкций, материалов и оборудования.
- Специальные требования к строительству сложных и уникальных сооружений.
- Сведения об усл. произв-ва СМР на реконструируемых объектах.
- Объемно-планировочные и конструктивные решения зданий и сооружений и основные технологические схемы производства основных комплексов СМР.
- Сведения об условиях обеспечения строительства кадрами.
- Сведения об условиях обеспечения транспортом.
- Сведения о дислокации, мощностях и специализации генподрядных организаций данного территориального региона и возможности их перебазирования.
- Сведения об условиях обеспечения строительства жилыми и культурно-бытовыми зданиями.
- Сведения о наличии производственной базы стройиндустрии, номенклатуры выпускаемой ими продукции возможности максимального ее использования.
- Сведения об условиях строительства, предусмотренные контрактами с иностранными фирмами.
Для продолжения скачивания необходимо пройти капчу: