Временные параметры сетевой модели их расчет

Временные параметры сетевых графиков

В (табл. 1) приведены основные временные параметры сетевых графиков.

Таблица 1 – Временные параметры сетевых графиков

Элемент сети, характеризуемый параметром

Условное обозначение параметра

Ранний срок свершения события

Поздний срок свершения события

t_Р (i)

t_П (i)

Ранний срок начала работы

Ранний срок окончания работы

Поздний срок начала работы

Поздний срок окончания работы

Полный резерв времени работы

Свободный резерв времени работы

t_РН (i, j)

t_РО (i, j)

t_ПН (i, j)

t_ПО (i, j)

R_П (i, j)

R_С (i, j)

Продолжительность критического пути

t (L)

Событие не может наступить прежде, чем свершатся все предшествующие работы. Поэтому ранний срок t_Р (i) свершения i – того события определяется продолжительностью максимального пути, предшествующего этому событию: t_Р (i)=max t(L_Пi), где L_Пi – любой путь, предшествующий i – тому событию, то есть путь от исходного до i –того события сети.

Ранний срок свершения события i – это самый ранний срок, к которому завершаются все работы, предшествующие этому событию.

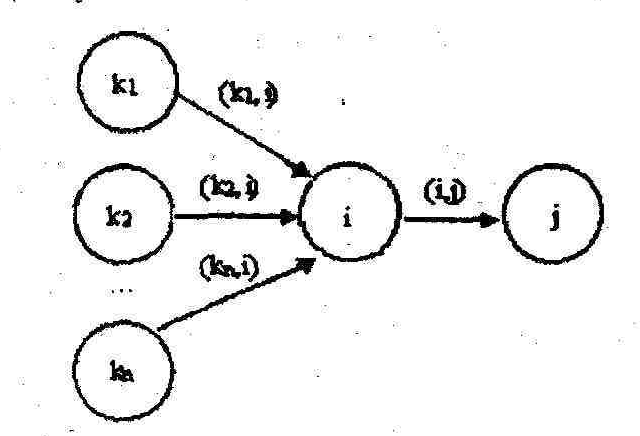
Если событие i имеет несколько предшествующих работ (рис.5), то ранний срок свершения события i находится так:

Пусть B(i) – множество работ, непосредственно предшествующих событию i. Тогда

t_Р (i)=max< t_Р (k)+ t (k,i)>,(k,i) B(i) (1)

Задержка свершения события i по отношению к своему раннему сроку не отразится на сроке свершения завершающего события (значит, и на сроке выполнения комплекса работ) до тех пор, пока сумма срока свершения этого события и длины максимального из последующих за ним путей не превысит длины критического пути.

Поэтому поздний срок t_П (i) свершения i – того события равен:

t_П (i)=t_КР – max t(L_ci), где L_ci – любой путь, следующий за i –м событием, то есть путь от i –того до завершающего события сети.

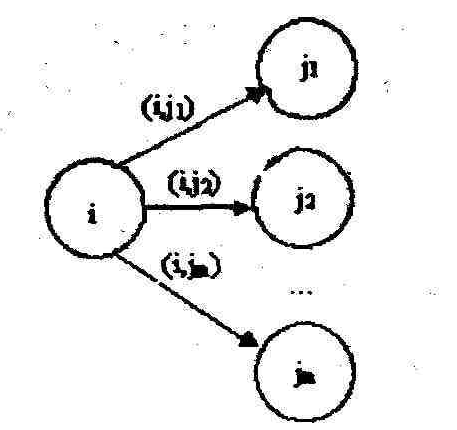
Если событие i имеет несколько последующих работ (рис. 6), то поздний срок свершения события i удобно находить по формуле:

t_П (i)= min< t_П (j)- t (j,i)>,(j,i) C(i) (2)

где: C(i) – множество работ (j,i), выходящих из вершины i.

При любом поздний срок свершения события i находится так: сначала при i=n полагают t_П (i)=t_Р(n) =t_КР, затем последовательно для i равным n-1, n-2,….1 вычисляют по формуле (2).

Резерв времени i – того события определяется как резерв между поздним и ранним сроком его свершения:

R_i = t_П(i) – t_Р(i) (3)

Резерв времени i – того события показывает, на какой допустимый срок можно задержать наступление этого события, не вызывая при этом увеличения времени выполнения комплекса работ.

Критические события резервов времени не имеют, так как любая задержка в свершении события, лежащего на критическом пути, вызовет такую же задержку в свершении завершающего события.

Из этого следует, что для определения критического пути (если он единственный) вовсе не обязательно перебирать все полные пути сетевого графика и определять их длины. Определив ранний срок наступления завершающего события сети, определяют длину критического пути, а выявив события с нулевыми резервами времени, определяют его конфигурацию.

Если критических путей несколько, то выявление их с помощью критических событий может быть затруднительно, так как через часть критических событий могут проходить как критические, так и некритические пути. В этом случае для определения критических путей следует использовать критические работы.

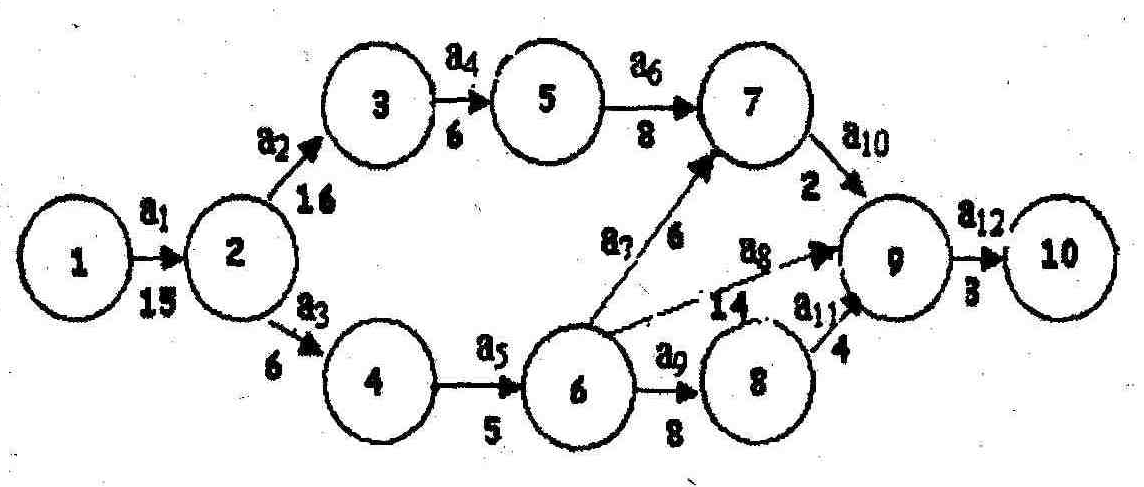
По (рис. 7) рассчитать ранние и поздние сроки свершения событий, а также их резервы. Найти критический путь выполнения комплекса работ и его длину.

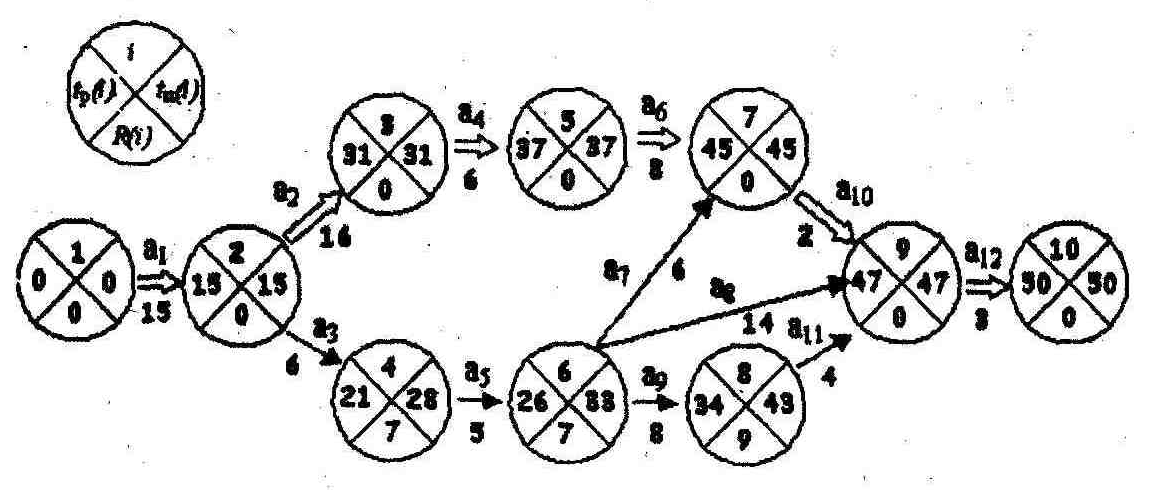
Каждую вершину сети разбиваем на четыре сектора. В верхней части сектора отмечается номер события i, в левой – ранний срок свершения события i, в правой – поздний срок свершения события i, в нижней – резерв времени этого события (рис. 8).

Сначала по формуле (1) находим ранние сроки свершения события i и заносим их в левые секторы сетевого графика. Имеется:

Теперь рассчитываются поздние сроки свершения событий. Расчет начинается с последнего события и затем, «пятясь», двигается к первому событию.

Для i=10 поздний срок свершения события t_П (10)= t_Р (10)=47+3=50. Далее по формуле (2) имеется:

Результаты расчета заносят в правые секторы вершин сети.

По формуле (3) рассчитывают резервы времени каждого события и заносят их в нижние секторы вершин.

R(1) =0-0=0;

R(2) =15-15=0;

Чтобы рассчитать критический путь фиксируются события, не имеющие резервов времени. Это события 1,2,3,5,7,9,10. Следовательно, путь 1→2→3→5→7→9→10 является критическим.

Длина критического пути t_КР= t_Р (10)=50.

Критический путь отмечается на сетевом графике двойной стрелкой.

Источник

Методы расчета временных параметров и критического пути сетевой модели проекта

Если размеры сетевого графика невелики, то его временные параметры и критический путь могут быть найдены путем непосредственного рассмотрения графика вершина за вершиной, работа за работой. Но, естественно, по мере увеличения масштабов модели вероятность появления ошибки в расчетах будет возрастать в геометрической прогрессии. Поэтому, даже при небольших размерах модели целесообразно воспользоваться одним из наиболее подходящих алгоритмических методов расчета, позволяющих подойти к этой задаче формально.

Самыми распространенными методами расчета временных параметров сетевой модели являются табличный и матричный. Поэтому, даже если исходная информация по сетевой модели представлена в виде сетевого графика или временной диаграммы, приступая к анализу, ее следует привести к табличной либо матричной форме.

В качестве примера будем рассматривать модель, заданную изначально сетевым графиком, приведенным на рис. 6.

Рисунок 6. Пример сетевого графика для иллюстрации методов расчета временных параметров

Как табличный, так и матричный метод расчета временных параметров сетевой модели основывается на следующих соотношениях, вытекающих из определений временных параметров. Для удобства понимания индекс работы, как правило, состоит из двух букв, например, [ij], первая из которых соответствует индексу начального события работы, а вторая – индексу конечного события работы. С учетом этого замечания:

• Раннее время начала работы [ij] совпадает с ранним временем наступления события [i], т.е. ESTij = EET [i].
• Позднее время окончания работы [ij] совпадает с поздним временем наступления события [j], т.е. LFTij = LET [j].
• Раннее время окончания работы [ij]:

• Позднее время начала работы [ij]: LSTij = LFTij – tij.
• Раннее время наступления события [j] совпадает с самым поздним (максимальным) ранним временем окончания из всех тех работ, для которых данное событие является конечным, т.е. EET[j] = max , где [rj], [nj], . [mj] – индексы работ, для которых событие [j] является конечным.
• Позднее время наступления события [j] совпадает с самым ранним (минимальным) поздним временем начала из всех тех работ, для которых данное событие является начальным, т.е. LET[j] = min < LSTjr, LSTjn, . LSTjm>, где [jr], [jn], . [jm] – индексы работ, для которых событие [j] является начальным.
• Для исходного и заключительного события сетевой модели справедливо: EET[s] = LET[s]
• Но если для исходного события принимается, как правило, момент времени, равный 0, то для заключительного события он появляется в результате расчетов и по нему можно судить о продолжительности критического пути. Итак, для заключительного события справедливо: EET[f] = LET[f] = TK, где TK – продолжительность критического пути.
• Полный резерв времени выполнения работы [ij]: TFij = LЕT[j] – EET[i] – tij.
• Свободный резерв времени выполнения работы [ij]: FFij = EЕT[j] – EET[i] – tij.
• Независимый резерв времени выполнения работы [i]: IFi = EЕT[j] – LET[i] – tij.

Источник

Параметры сетевых моделей и методы их расчета

Сетевая модель имеет ряд характеристик, которые позволяют определить степень напряженности выполнения отдельных работ, а также всего их комплекса и принять решение о перераспределении ресурсов.
Ранний срок наступления события t_р(i) — самый ранний из возможных сроков наступления события. Он равен продолжительности максимального пути от исходного события до данного.
t_р(i) = max t[L_р(i)] (2.1)
Например, t_р(7)=19, т.к. L₁=(1,2,4,7), L₂=(1,3,4,7),
t(L₁)=5+12=17 < t(L₂)=7+12=19.
Ранний срок начала работы t_р.н.(i,j) равен продолжительности максимального пути от исходного до начального события данной работы.
t_р.н.(i,j)=max t[L_n(i)](2.2)
Например, t_р.н.(7,11)=19, т.к. L₁=(1,2,4,7), L₂=(1,3,4,7),
t(L₁)=5+12=17 2)=7+12=19.
Ранний срок начала работы равен раннему сроку наступления начального события данной работы.
t_р.н.(i,j) = t_р(i) (2.3)
Ранний срок окончания работы t_р.о.( i,j) равен сумме раннего срока начала работы и продолжительности данной работы.
t_р.о.(i,j)= t_р.н.(i,j) + t(i,j) (2.4)
Например, t_р.о.(7,11)= t_р.н.(7,11) + t(7,11)= 19+8=27.
Поздний срок наступления события t_п( i) равен разности между продолжительностью критического пути и продолжительностью максимального пути от данного события до завершающего.
t_п(i) =T_кр — max t[L_к(i)](2.5)
Например, t_п(7)=19, т.к. L₁=(7,11), L₂=(7,9,11), t(L₁)=8 > t(L₂)=4,
t_п(7) = T_кр — max t[L_к(7)]=27 — 8=19.
Для событий критического пути t_р( i)=t_п(i), для других событий t_р(i)t_п(i).
Поздний срок окончания работы t_п.о.( i,j) – это самый поздний срок окончания работы, при котором планируемый срок окончания проекта не меняется, он равен разности между продолжительностью критического пути и продолжительностью максимального пути от конечного события данной работы до завершающего события.
t_п.о.(i,j)=T_кр — max t[L_к(j)] (2.6)
Поздний срок окончания работы равен позднему сроку наступления конечного события t_п.о.(i,j) = t_п(j). Например, t_п.о.(4,7) = t_п(7)=19.
Поздний срок начала работы t_п.н.( i,j) – самый поздний срок начала работы, при котором планируемый срок окончания проекта не меняется.
t_п.н.(i,j)= t_{п .о.}(i,j) — t(i,j) (2.7)
Например, t_п.н.(4,7)= t_п.о.(4,7) — t(4,7)=19-12=7.
Для работ критического пути ранние и поздние сроки начала и окончания работ равны: t_р.н.(4,7)= t_п.н.(4,7)=7, t_р.о.(4,7)= t_п.о.(4,7)=19.
Работы, не лежащие на критическом пути, могут иметь резервы времени.
Полный резерв времени R_п( i,j) – максимальное время, на которое можно увеличить продолжительность данной работы, не изменяя продолжительности критического пути.
R_п (i,j)= t_п(j) — t_р(i) — t(i,j)
R_п(i,j)= t_п.н (i,j) — t_р.н.(i,j) (2.8)
R_п (i,j)= t_п.о.(i,j) — t_р.о.(i,j)
Свободный резерв времени R_с( i,j) равен разности между ранним началом последующей работы и ранним окончанием рассматриваемой работы.
R_с(i,j)= t_р.н (j,к) — t_р.о.(i,j) (2.9) Перейти к онлайн решению своей задачи

Источник