Математическое представление нейронных сетей
Продолжаем «неделю нейронных сетей». В этом посте вы узнаете о нейронных сетях на примерах математических моделей. Говоря проще, вы узнаете о том, как представить нейронные сети с помощью математических уравнений. Дата-сайентисту или исследователю машинного обучения было бы неплохо получить представление о том, как нейронные сети могут быть преобразованы в кучу математических уравнений, для вычисления различных значений. Хорошее понимание представления выходных данных функции активации различных вычислительных блоков (узлов, нейронов) в разных слоях может помочь быстрее и лучше понять алгоритм обратного распространения.
Под катом — простое и краткое введение в математическое представление нейронных сетей для интересующихся теорией практиков: от перцептрона до сети с двумя скрытыми слоями.
Однослойная нейронная сеть (перцептрон)
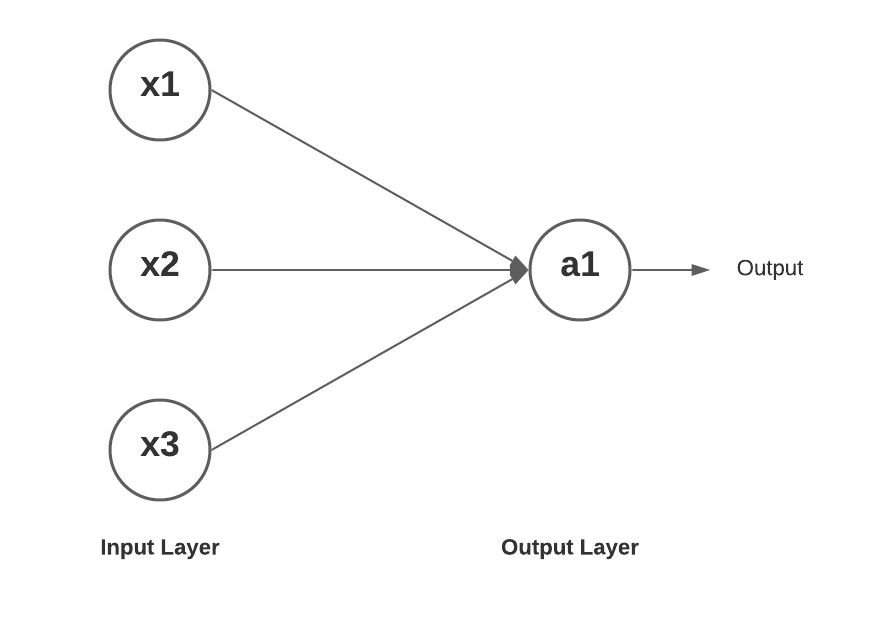
Вот как выглядит однослойная нейронная сеть. А вот тут можно почитать, как эта сеть объяснена с помощью примера на Python.
Перцептрон — однослойная нейронная сеть
Вот как могло бы выглядеть математическое уравнение для получения значения a1 (выходной узел) в качестве функции входных x1, x2, x3 .
В приведенном выше уравнении верхний индекс веса представляет слой, а нижний индекс весов представляет вес соединения между входным и выходным узлами. Таким образом, представляет вес первого уровня между узлом 1 в следующем слое и узлом 2 в текущем слое.
Нейронная сеть с одним скрытым слоем
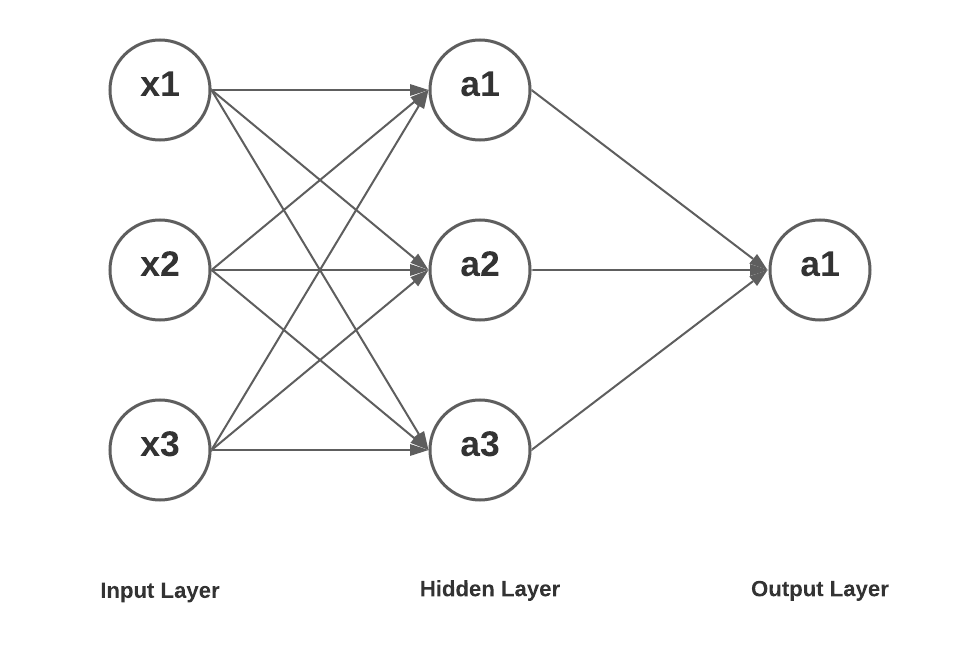
Ниже нейронная сеть с одним скрытым слоем, имеющим три нейрона, входным слоем с тремя входными нейронами и выходным слоем с одним нейроном.
Нейронная сеть с входным, скрытым и выходным слоями
Вот так может выглядеть математическое уравнение для получения значения a1, a2 и a3 в слое 2 в качестве функции входных x1, x2, x3 . Кроме того, значение a1 в слое 3 представлено как функция значений a1, a2 и a3 в слое 2.
Сначала давайте представим выходные значения, обработанные в трех скрытых нейронах скрытого слоя. Входной слой представлен как слой 1, скрытый слой как слой 2 и выходной слой — это слой 3.
Определим выходное значение узла в выходном слое. Значение представляется как функция от a1, a2 и a3 в предыдущих узлах, которые могут быть представлены как значения x1, x2 и x3 во входном слое.
Нейронная сеть с одним скрытым слоем (3 нейрона) и выходным слоем (2 нейрона)
Ниже представлена нейронная сеть с одним скрытым слоем, имеющим три нейрона, входным слоем с двумя входными нейронами, а также выходным слоем с двумя нейронами.
Трехслойная нейронная сеть
Вот так может выглядеть математическое уравнение для получения значения a1, a2, a3 в слое 2 в качестве функции входных значений x1, x2 . Кроме того, значение a1, a2 в слое 3 представлено как функция значений a1, a2, a3 в слое 2.
Сначала давайте представим выходные значения, обработанные в трех скрытых нейронах скрытого слоя. Входной слой представлен как слой 1, скрытый слой как слой 2 и выходной слой — это слой 3.
Определим выходное значение узлов в выходном слое. Значение представляется как функция от a1, a2, a3 в предыдущих узлах, которые могут быть представлены как значения x1, x2, x3 во входном слое.
Сети глубокого обучения с двумя скрытыми слоями
Наконец, давайте посмотрим, как выходные значения узлов a1 в выходном слое могут быть выражены в виде математических вычислений как функция входных сигналов x1, x2 . Вот схема сети глубокого обучения, имеющей два скрытых слоя, один из которых имеет три узла, а другой — два узла. Затем имеется входной уровень с двумя входными узлами, и выходной слой с одним выходным узлом. Вот схема упрощенной сети глубокого обучения.
Нейронная сеть глубокого обучения
Значения в слое 2 ( a1, a2, a3 ) и слое 3 ( a1, a2 ) останутся такими же, как в предыдущем разделе. Давайте представим значение 1 в выходном слое как функцию значений a1 и a2 в предыдущем слое (слой 3).
Заключение
Ниже краткое изложение того, что вы узнали в этом посте о представления нейронных сетей в виде математических моделей:
- Важно понимать обозначения, в которых вы будете представлять нейронную сеть как уравнение.
- Первому или входному слою можно назначить номер 1, скрытому номер 2, а выходному 3.
- Весам между входным узлом в одном слое и узлом в следующем слое назначается верхний индекс — значение слоя, состоящего из входного узла. Нижний индекс веса состоит из двух чисел — числа, представляющего узел в следующем слое и номера входного узла.