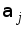Сетевой_курс_НИС_2012 / Модуль 13 / Информационные системы как системы массового обслуживания
Проектирование любой системы можно рассматривать как решение последовательности проектных задач, которые включают задачи синтеза и задачи анализа системы и ее частей.
В настоящее время в терминах систем массового обслуживания (СМО) описываются многие реальные системы: вычислительные системы, узлы сетей связи, диспетчерские системы посадки самолетов, магазины, производственные участки, любые автоматизированные системы и системы материального производства, Интернет, банкоматы, где возможны очереди и (или) отказы в обслуживании.
В автоматизированной производственной системе роль обслуживающего «прибора» может играть ЭВМ любого уровня, которая перенаправляет потоки заготовок, инструментов, оснастки и пр. по различным компонентам производственных систем (а реально – перенаправляет потоки управляющих команд) или оборудование, которое производит обработку или сборку изделий. Роль заявок играют решаемые задачи, команды, заготовки и полуфабрикаты, инструмент и оснастка и т.д. Заявки-команды поступают из центральной ЭВМ, управляющей всей данной технической системой. Заявки в виде обрабатываемых заготовок и полуфабрикатов, инструмента и оснастки поступают на технологическое оборудование из автоматизированной транспортно-скаладской системы.
В настоящее время теорию систем массового обслуживания используют для определения важнейших системных характеристик технических автоматизированных систем: производительности; времени доставки заявок; вероятности отказа функционирования системы; области допустимых значений нагрузки, при которых обеспечивается требуемое качество обслуживания и др.
Система массового обслуживания как модель
Дадим краткое описание системы массового обслуживания.
Заявки (требования) на обслуживание поступают через постоянные или случайные интервалы времени.
Приборы (каналы) служат для обслуживания этих заявок. Обслуживание длится некоторое время, постоянное или случайное. Если в момент поступления заявки все приборы заняты, заявка помещается в ячейку буфера и ждет там начала обслуживания.
Заявки, находящиеся в буфере, составляют очередь на обслуживание. Если все ячейки буфера заняты, заявка получает отказ в обслуживании и может не пройти обработку (теряется).
Вероятность потери заявки (вероятность отказа) одна из основных характеристик СМО. Другие характеристики: среднее время ожидания начала обслуживания, средняя длина очереди, коэффициент загрузки прибора (доля времени, в течение которого прибор занят обслуживанием) и т.д.
В зависимости от объема буфера различают СМО с отказами, где нет буфера, СМО с ожиданием, где буфер не ограничен (например, очередь в магазин на улице, бесконечно длинный конвейер в ГПС) и СМО смешанного типа, где буфер имеет конечное число заявок. В СМО с отказами нет очереди, в СМО с ожиданием нет потерь заявок, в СМО смешанного типа то и другое возможно.
Математические модели простейших систем
массового обслуживания
Ниже будут рассмотрены примеры простейших систем массового обслуживания (СМО). Понятие «простейшие» не означает «элементарные». Математические модели этих систем применимы и успешно используются в практических расчетах. Каждый вариант системы массового обслуживания имеет свои показатели функционирования.
Одноканальная СМО с отказами
Рассмотрим такую задачу: локальная сеть имеет один сервер, на который с постоянной интенсивностью на обработку поступают заявки о пользователей. Если сервер занят, то заявка перенаправляется в компьютер, который выполняет роль резервного сервера. Интенсивность обслуживания заявок в головном сервере постоянна и равна . Определить основные показатели работы данной системы.
Переформулируем нашу задачу в общепринятых для систем массового обслуживания терминах.
Дано: система имеет один канал обслуживания, на который поступает простейший поток заявок с интенсивностью . Поток обслуживаний имеет интенсивность . Заявка, заставшая систему занятой, сразу же покидает ее.
Найти: абсолютную и относительную пропускную способность СМО и вероятность того, что заявка, пришедшая в случайный момент времени t, получит отказ.
Решение: система в любой момент времени t может находиться в двух состояниях: S0 – канал свободен; S1 – канал занят. Переход из S0 в S1 связан с появлением заявки и немедленным началом ее обслуживания. Переход из S1 в S0 осуществляется, как только очередное обслуживание завершится. Граф состояний системы показан на рисунке ниже.
Выходные характеристики (характеристики эффективности) функционирования этой и других СМО будут даваться далее без выводов и доказательств.
Абсолютная пропускная способность (среднее число заявок, обслуживаемых в единицу времени):
где – интенсивность потока заявок (величина, обратная среднему промежутку времени между поступающими заявками — );
– интенсивность потока обслуживаний (величина, обратная среднему времени обслуживания )
Относительная пропускная способность (средняя доля заявок, обслуживаемых системой):
Вероятность отказа (вероятность того, что заявка покинет СМО необслуженной):
Очевидны следующие соотношения:
.
Пример №1. На вход системы поступают заявки на обработку в среднем через 0,5 часа . Среднее время обработки одной заявки равно . Если при поступлении заявки на обработку система занята, то она (заявка) направляется в другую систему. Найти абсолютную и относительную пропускную способности системы и вероятность отказа по изготовлению детали.
Т.е. в среднем примерно 46 % заявок обрабатываются в этой системе.
.
Т.е. в среднем примерно 54 % заявок направляются на обработку в другую систему.
Одноканальная СМО с неограниченной очередью
На практике довольно часто встречаются одноканальные СМО с очередью (врач, обслуживающий пациентов; одноканальный телефон; ЭВМ, выполняющая заказы пользователей, изделия в очереди на обработку или упаковку и т.д.).
Рассмотрим такую задачу: система имеет одну единицу технологического оборудования, на которое с постоянной интенсивностью на упаковку поступают готовые изделия с автоматизированного конвейера. Если оборудование занято, то с конвейера изделие не перенаправляется никуда, а ждет своей очереди. Интенсивность обслуживания изделий при упаковке постоянна (изделия одинаковые) и равна . Определить основные показатели работы данной системы.
Переформулируем нашу задачу в общепринятых для систем массового обслуживания терминах.
Пусть имеется одноканальная СМО с очередью, на которую не наложено никаких ограничений (ни по длине очереди, ни по времени ожидания). На эту СМО поступает поток заявок интенсивностью ; поток обслуживаний имеет интенсивность . обратную среднему времени обслуживания заявки tоб. Требуется найти финальные вероятности состояний СМО, а также характеристики ее эффективности:
Lсист — среднее число заявок в системе;
Wсист — среднее время пребывания заявки в системе;
Lоч — среднее число заявок в очереди;
Wоч — среднее время пребывания заявки в очереди;
Pзан — вероятность того, что канал занят (степень загрузки канала).
Что касается абсолютной пропускной способности А и относительной Q, то вычислять их нет надобности: в силу того, что очередь не ограничена, каждая заявка раньше или позже будет обслужена, поэтому А=, по той же причине Q=1.
Решение. Состояния системы будем нумеровать по числу заявок, находящихся в СМО:
S1, — канал занят, очереди нет;
S2 — канал занят, одна заявка стоит в очереди и т.д.
Теоретически число состояний ничем не ограничено.
Э то — схема гибели и размножения, но с бесконечным числом состояний. По всем стрелкам поток заявок с интенсивностью переводит систему слева направо, а справа налево — поток обслуживаний с интенсивностью . Если >, то канал с заявками не справляется, очередь растет до бесконечности. Если < , то задача вполне разрешима. Воспользуемся формулами для финальных вероятностей из схемы гибели и размножения и для бесконечного числа состояний. Подсчитаем финальные вероятности:
В этой формуле p равно отношению (интенсивности поступления) к (интенсивности обслуживания). Ряд в этой формуле представляет собой геометрическую прогрессию. При р < 1 ряд сходится; при р > 1 ряд расходится. Теперь предположим, что условие сходимости выполнено и р
Откуда вероятности P1, P2, ….определяются по формулам
Как видно, вероятности Р0, Р1. образуют геометрическую |прогрессию со знаменателем р. Как ни странно, максимальная из них P0 -вероятность того, что канал будет вообще свободен. Как бы ни была загружена система с очередью, если только она вообще справляется с потоком заявок, самое вероятное число заявок в системе будет равно нулю.
Найдем среднее число Lсист заявок в СМО. Случайная величина Z— число заявок в системе, имеет возможные значения 0,1,2. c вероятностями Р0, Р1, …..Рк. Ее математическое ожидание
П осле преобразований получаем
Найдем среднее время пребывания заявки в системе
Найдем среднее число заявок в очереди Lоч. Будем рассуждать так: число заявок в очереди равно числу заявок в системе минус число заявок, находящихся под обслуживанием. Значит по правилу сложения математических ожиданий, среднее число заявок в очереди Lоч равно среднему числу заявок в системе Lсист минус среднее число заявок под обслуживанием. Число заявок под обслуживанием может быть либо нулем (канал свободен), либо единицей (канал занят). Математическое ожидание такой случайной величины равно вероятности того, что канал занят (Рзан). Очевидно, Рзан) равно 1 минус вероятность Р0 того, что канал свободен:
Следовательно, среднее число заявок под обслуживанием равно
С реднее время пребывания заявки в очереди
2.3. Сети массового обслуживания
Сеть массового обслуживания представляет собой совокупность конечного числа N обслуживающих узлов, в которой циркулируют заявки, переходящие в соответствии с маршрутной матрицей из одного узла в другой.
Узел всегда является разомкнутой СМО (причем СМО может быть любого класса). Отдельные СМО отображают функционально самостоятельные части реальной системы, связи между СМО структуру системы, а требования, циркулирующие по СеМО, составляющие материальных потоков.
СеМО классифицируют по нескольким признакам (рис. 2.5).
Сеть называется линейной, если интенсивности потоков заявок в узлах связаны между собой линейной зависимостью 


Коэффициент (коэффициент передачи) характеризует долю заявок, поступающих вj-й узел от источника заявок, либо среднее число прохождений заявки через данный узел за время ее нахождения в сети.
Если интенсивности потоков заявок в узлах сети связаны нелинейной зависимостью (например, ), то сеть называется нелинейной.
Сеть всегда линейна, если в ней заявки не теряются и не размножаются.
Рис. 2.5. Классификация СеМО
Разомкнутая сеть – это такая отрытая сеть, в которую заявки поступают из внешней среды и из которой уходят после обслуживания во внешнюю среду. Особенностью разомкнутой СеМО (РСеМО) является наличие одного или нескольких независимых внешних источников, которые генерируют заявки, поступающие в сеть, независимо от того, сколько заявок уже находится в сети. В любой момент времени в РСеМО может находиться произвольное число заявок (от 0 до ).
В замкнутой СеМО (ЗСеМО) циркулирует фиксированное число заявок, а независимый внешний источник отсутствует. Исходя из физических соображений, в ЗСеМО выбирается внешняя дуга, на которой отмечается псевдонулевая точка, относительно которой могут измеряться временные характеристики. Число заявок в замкнутой сети постоянно.
Комбинированная сеть – это сеть, в которой постоянно циркулирует определенное число заявок и есть заявки, поступающие от внешних независимых источников.
В однородной сети циркулируют заявки одного класса. В неоднородной сети могут присутствовать заявки нескольких классов. Заявки относятся к разным классам, если они различаются хотя бы одним из следующих атрибутов:
– законом распределения длительности обслуживания в узлах;
– маршрутами (путями движения заявок в сети).
В экспоненциальной сети длительности обслуживания во всех узлах распределены по экспоненциальному закону и потоки, поступающие в разомкнутую сеть, простейшие (пуассоновские). Во всех остальных случаях сеть является неэкспоненциальной.
Если хотя бы в одном узле осуществляется приоритетное обслуживание, то это – приоритетная сеть. Приоритет – это признак, определяющий очередность обслуживания. Если заявки в узлах обслуживаются в порядке поступления, то такая сеть называется бесприоритетной.
Таким образом, экспоненциальной будем называть СеМО, отвечающую следующим требованиям:
– входные потоки СеМО пуассоновские;
– во всех N СМО время обслуживания заявок имеет экспоненциальную функцию распределения вероятностей, заявки обслуживаются в порядке прихода;
– переход заявки с выхода i-й на вход j-й СМО является независимым случайным событием, имеющим вероятность 
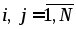

Для наглядного представления СеМО используется граф, вершины которого (узлы) соответствуют отдельным СМО, а дуги отображают связи между узлами.