ОПТИМИЗАЦИЯ СЕТЕВОЙ МОДЕЛИ ПО КРИТЕРИЮ «ВРЕМЯ – ЧИСЛО ИСПОЛНИТЕЛЕЙ»
Во многих областях экономики, технологии, проектирования, строительства, научных исследований особое значение имеет оптимизация распределения ресурсов, в том числе трудовых, при реализации новых проектов, когда выполняется огромное количество взаимозаменяемых операций, в работу вовлекается множество работников, предприятий, организаций. В таких задачах управление работами осложняется новизной разработки, трудностью точного определения сроков и затрат ресурсов на том или ином этапе. В этих случаях высокоэффективными инструментами управления являются сетевые методы и модели.
После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.
Минимизация числа исполнителей проекта при сохранении времени его выполнения. В ходе выполнения комплекса работ занятость работников различной квалификации и разных специальностей оказывается неравномерной. Это приводит к завышению потребности в них с одновременным снижением среднего уровня занятости и, как следствие, к перерасходу заработной платы и увеличению стоимости всего проекта.
Наиболее часто на практике приходится оптимизировать сетевой график при ограниченном ресурсе исполнителей определенной категории. Оптимизация по численности исполнителей основана на сдвиге работ в пределах имеющихся у них резервов времени. Ее целью является обеспечение наиболее равномерной занятости работников в течение всего времени выполнения проекта при сохранении общей продолжительности проекта.
Для проведения такой оптимизации часто применяется простой и наглядный графический метод. Согласно сетевой модели составляются линейная диаграмма (график привязки) и карта проекта (график загрузки).
На линейной диаграмме работы отмечают на оси ординат, располагая их снизу вверх по нарастанию индексов. На ось абсцисс наносится равномерная шкала времени (чаще в днях). Каждая работа вычерчивается в масштабе отрезком прямой, длина которой равна продолжительности работы.
Работы критического пути выделяются двойными линиями. Под стрелкой, изображающей работу, помещается в виде висящего флажка численность работников каждой категории, занятых выполнением данной работы. В исходной диаграмме все работы начинаются в свои ранние сроки, а фиктивная работа обозначается точкой.
Проверкой правильности построения линейной диаграммы является срок окончания последней работы проекта, совпадающий с длительностью критического пути. Практическая ценность графика привязки заключается в том, что с его помощью можно улучшать эффективность использования ресурса рабочей силы.
Карта проекта (график загрузки, график ежедневной потребности работников соответствующих категорий) для удобства построения и анализа строится под линейной диаграммой. Для каждого дня определяется суммарное количество исполнителей, занятых на параллельных работах проекта, и откладывается в масштабе по оси ординат. При этом часть исполнителей, занятых на работах критического пути, выделяется пунктиром и штриховкой. Для каждой категории исполнителей строится своя карта проекта. Далее проводится анализ их занятости.
Оптимизация ресурса рабочей силы заключается в одновременном решении двух задач:
минимизировать количество одновременно занятых исполнителей;
выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.
Оптимизация осуществляется перемещением части работ (имеющих резерв времени) с наиболее нагруженных (пиковых) дней на дни, имеющие наименьшую занятость исполнителей. После сдвига работы, работники выполняют ее уже в другие дни, и поэтому для каждого дня изменяется количество исполнителей, занятых одновременно. При оптимизации следует придерживаться следующих рекомендаций:
перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.
Различие в использовании свободных и полных резервов заключается в том, что при сдвиге работы с использованием свободного резерва моменты начала последующих за ней работ остаются неизменными (т. е. последующие работы не сдвигаются). При перемещении работы с использованием полного резерва, все последующие работы также сдвигаются.
Оптимизация проводится поэтапно, начиная с участков наибольшей и наименьшей занятости исполнителей. Все линейные диаграммы и карты проекта изображаются аналогично исходным. Число этапов оптимизации зависит от сложности проекта и квалификации корректировщика.
Рассмотрим графический метод на примере оптимизации сетевого графика, представленного табл. 4.1 и рис.4.1. Его необходимо оптимизировать по числу исполнителей (для простоты в примере принята одна категория исполнителей).
Исходные данные выполнения проекта
| Содержание работы | Работа | Длительность, дн. | Количество исполнителей |
| Разработка технических условий на аппарат | 1-2 | 4 | 5 |
| Разработка конструкции аппарата | 2-3 | 6 | 3 |
| Определение поставщиков узлов | 2-4 | 5 | 6 |
| Оформление заказа на покупные узлы | 2-7 | 11 | 6 |
| Разработка чертежей | 3-5 | 9 | 1 |
| Приемка узлов | 4-6 | 9 | 2 |
| Проектирование модели | 5-7 | 11 | 3 |
| Изготовление опытного образца | 6-7 | 10 | 5 |
| Испытание опытного образца | 7-8 | 4 | 6 |
| Поздний срок свершения события |
| Номер события |
| Ранний срок свершения события |
| Резерв времени |
| 9 |
| 5 |
| 11 |
| 4 |
| 10 |
| 11 |
| 9 |
| 6 |
| 4 |
| 1 0 0 0 |
| 2 4 4 0 |
| 7 30 30 0 |
| 8 34 34 0 |
| 3 10 10 0 |
| 5 19 19 0 |
| 4 9 11 2 |
| 6 18 20 2 |
Рис. 4.1. Пример сетевого графика
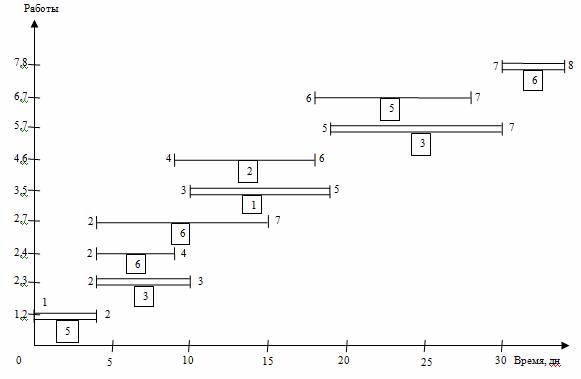
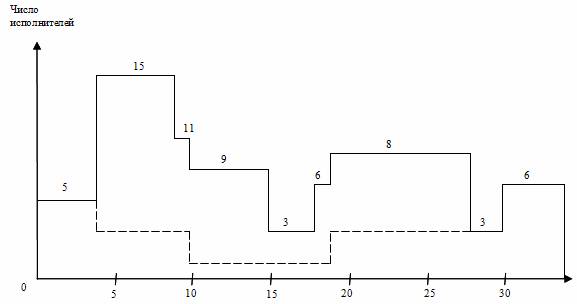
Согласно рекомендациям составим линейную диаграмму и карту проекта (график ежедневной потребности ресурса) и проведем предварительный анализ занятости исполнителей (рис. 4.2). По графику ежедневной потребности видно, что в разные дни выполнения проекта наблюдается различная занятость исполнителей: сначала их требуется 5 (1-4 дни), затем 15 (5-10 дни), потом только 3 (16-18 дни), снова 8 (20-28 дни), вновь 3 (29-30 дни) и в завершение 6 (31-34 дни). Таким образом, имеем явную неравномерность занятости исполнителей (то перегружены, то недогружены работой).
| работы |
| время, дн |
| время, дн |
| чел. |
Рис. 4.2. Линейная диаграмма и карта проекта до оптимизации
| время, дн |
| время, дн |
| чел. |
| работы |
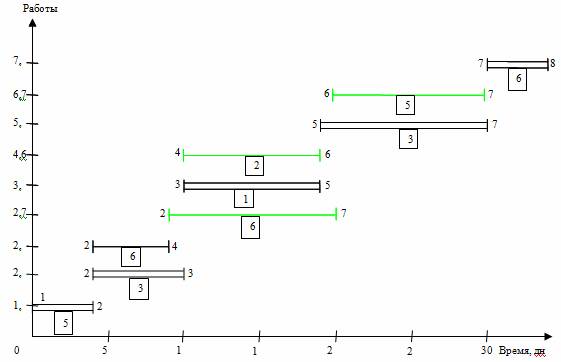
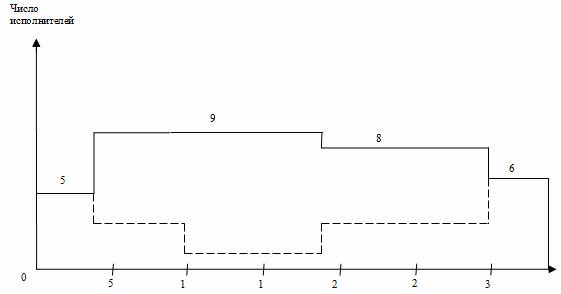
Рис. 4.3. Линейная диаграмма и карта проекта после оптимизации
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.
15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 4.3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено.
ЗАДАЧИ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ
СОГЛАСНО ВАРИАНТАМ
Требуется оптимизировать процесс организации работ по числу исполнителей. Содержание и продолжительность выполнения работ по организации экспериментального производства представлена в таблице:
Оптимизация сетевой модели по критерию время – число исполнителей
После построения сетевого графика и определения его временных параметров проводят проверку соответствия полученных сроков продолжительности разработки нормативным или директивным срокам. Далее анализируют структуру сетевой модели, выявляя неоднородность напряженности работ проекта.
В настоящее время на практике сетевую модель вначале корректируют по времени, т. е. приводят ее к заданному сроку окончания проекта. Затем приступают к корректировке графика по критерию распределения ресурсов, начиная с трудовых ресурсов.
Минимизация числа исполнителей проекта при сохранении времени его выполнения
- минимизировать количество одновременно занятых исполнителей;
- выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.
- перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
- работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
- работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
- перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
- передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.
Рис. 1. Пример сетевого графика
Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.
Рис. 2. Линейная диаграмма и карта проекта до оптимизации
15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено. Видеоинструкция