- Задание 1 ЕГЭ по информатике. Информационные модели
- Граф (сетевая модель данных)
- Особенности анализа графов в решении задания №1 ЕГЭ
- Типы заданий
- Поиск оптимального маршрута по таблице
- Пример типового задания
- Решение задания
- Однозначное соотнесение таблицы и графа
- Типовое задание
- Решение
- Неоднозначное соотнесение таблицы и графа.
- Пример задания
- Решение задания
- Видеорешение задачи 1 ЕГЭ по информатике
- Подготовиться к ЕГЭ с репетитором
- Задача №7.5
- Сетевая модель задачи и ее решение.
Задание 1 ЕГЭ по информатике. Информационные модели
В заданиях этого раздела курса требуется установить соответствие между разными форматами данных, основными из которых являются таблицы и графы.
При решении задач на эту тему необходимо уметь преобразовывать таблицы в схемы и наоборот.
Граф (сетевая модель данных)
представляет собой набор вершин, соединенных ребрами, и чаще всего описывается в виде таблицы, например, матрицы смежности или весовой матрицы.
, такой, в котором ребрам присвоены веса, например, расстояние между городами или стоимость перевозки.
Особенности анализа графов в решении задания №1 ЕГЭ
Во многих задачах, вес указывает на длину пути между двумя точками.
в графе представляет собой количество ребер, соединенных с ней.
Чтобы определить степень вершины по заданной таблице (например, весовой матрице), необходимо посчитать количество ненулевых ячеек в соответствующей строке или столбце.
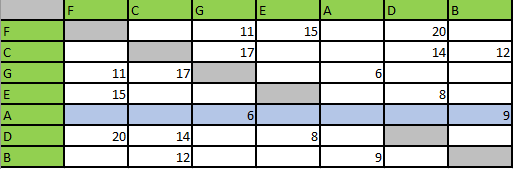
Например, степень вершины А равна 2, так как в строке А (выделена голубым) есть две ненулевые ячейки со значениями 6 и 9
В данном примере, . То есть, расстояние из пункта F в G равно расстоянию из G в F (11). Но, имеются задания с несимметричной матрицей.
Типы заданий
- Поиск оптимального маршрута по таблице.
- Однозначное соотнесение таблицы и графа.
- Неоднозначное соотнесение таблицы и графа.
Поиск оптимального маршрута по таблице
Пример типового задания
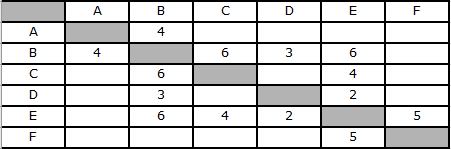
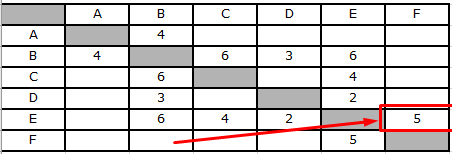
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет). Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).
Решение задания
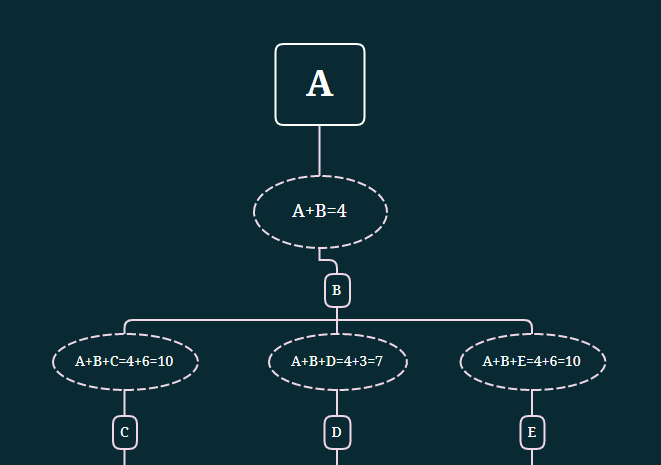
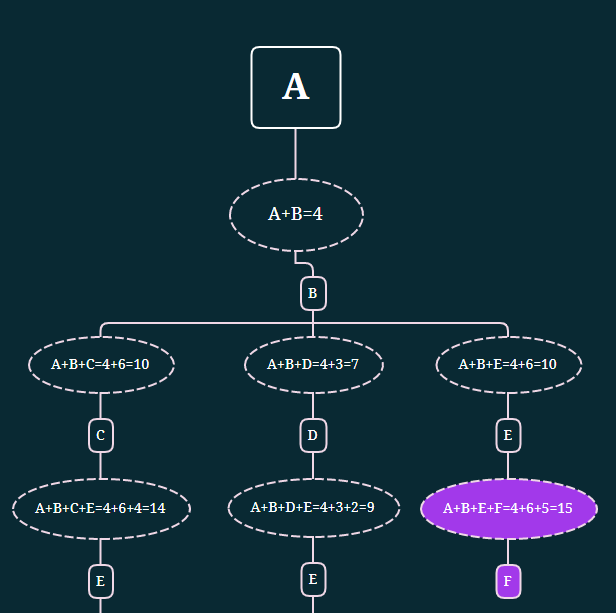
Для решения задания, необходимо построить дерево возможных маршрутов. В качестве вершин будут населенные пункты. Ветви дерева — расстояния между городами.
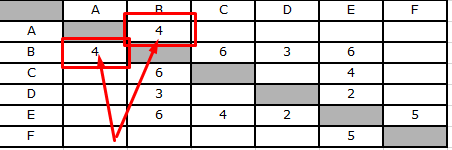
Исходя из данных таблицы, из пункта А в пункт В есть единственный маршрут длиной 4.
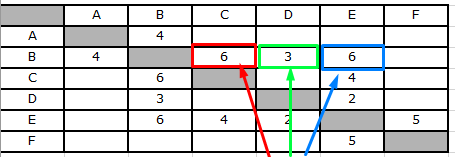
Из пункта B можно вернуться в A (что не имеет смысла, так как это удлинит маршрут), а также добраться до C, D, E. Из B в C, расстояние 6, в D — 3, а в E — 6.
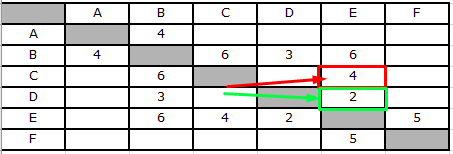
Из пунктов C и D можно добраться только в E:
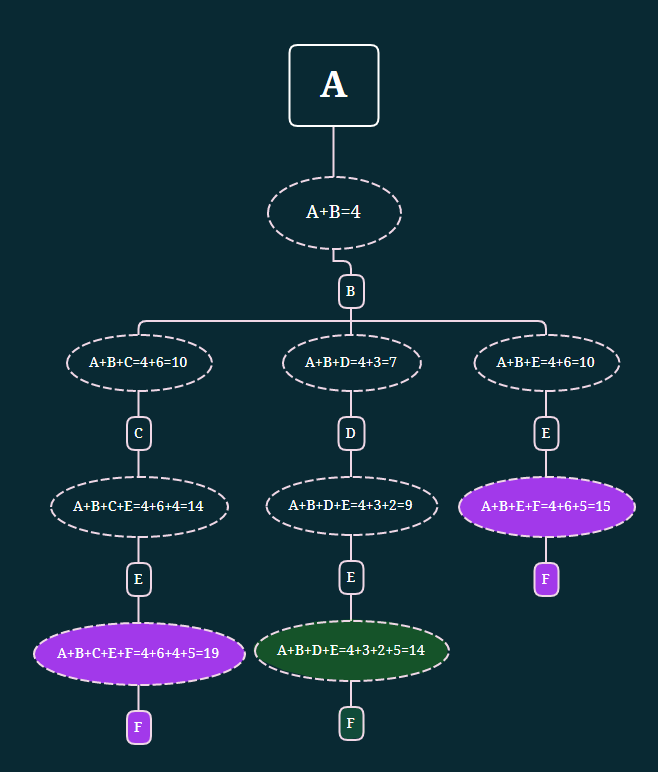
Из пункта E можно добраться в пункт F
Получилось 3 маршрута: ABCEF (длина 19), ABDEF (длина 14) и ABEF (15). Самый короткий маршрут — ABDEF длиной 14.
Однозначное соотнесение таблицы и графа
Особенность данных заданий в том, что необходимо по данным таблицы и графа, соотнести строки и столбцы таблицы с вершинами графа (сетевой модели). Здесь можно точно определить, для каждой вершины графа конкретную строку и столбец в таблице.
Типовое задание
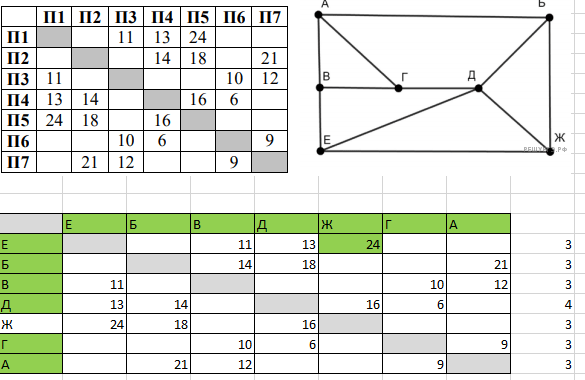
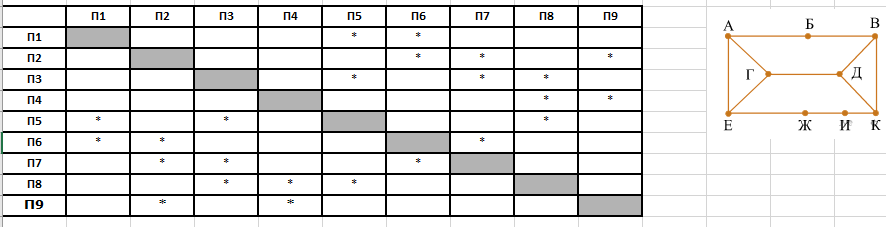
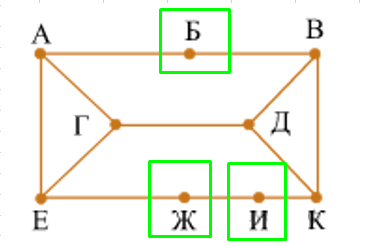
На рисунке схема дорог изображена в виде графа, в таблице звёздочками обозначено наличие дороги между населёнными пунктами. Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с буквенными обозначениями на графе. Укажите номера, которые могут соответствовать пунктам Г и Д. В ответе запишите эти номера в порядке возрастания без пробелов и знаков препинания.
Решение
Скопируем таблицу из задания в Excel вместе с рисунком графа. Это поможет нам быстро посчитать связность вершин, делать пометки (называть вершины) и выделять цветом промежуточные вычисления.
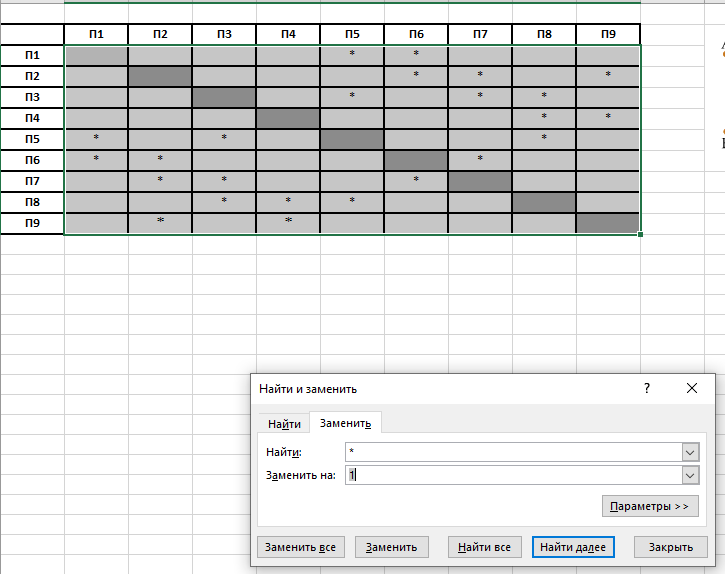
Чтобы посчитать связность вершин в таблице, заменим символы * на 1. Для этого, выделим таблицу (обязательно без названий строк и столбцов. ) нажмем Ctrl+H и сделаем замену (жмем «Заменить всё»):
Теперь вместо символов *, у нас стоят 1, и мы можем приступать к подсчету связности вершин. Для этого, будем использовать функцию СЧЕТ.
Функция СЧЕТ (ДИАПАЗОН1; ДИАПАЗОН2; ДИАПАЗОН3…), позволяет посчитать количество непустых ячеек в указанных диапазонах.
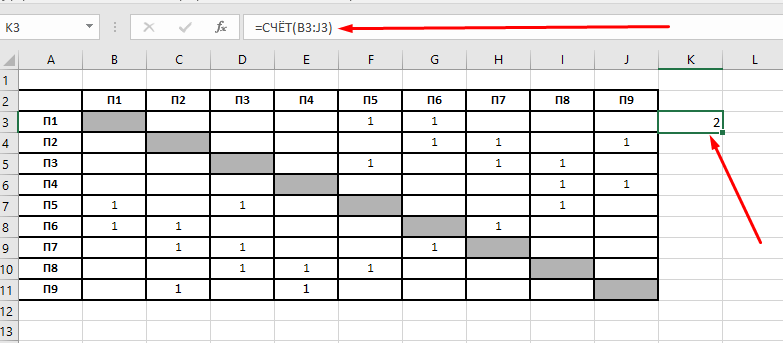
Посчитаем связность для строки П1. Для этого введем в ячейку K3 формулу: =СЧЁТ(B3:J3)
Размножим данную формулу для других строк таблицы. Для этого необходимо навести курсор мыши на угол ячейки K3 (где находится исходная формула).
Курсор сменится на значок черного крестика (как на рисунке)
После этого, зажимаем левую клавишу мыши и не отпуская, тянем вниз до самой последней строки (ячейки K11).
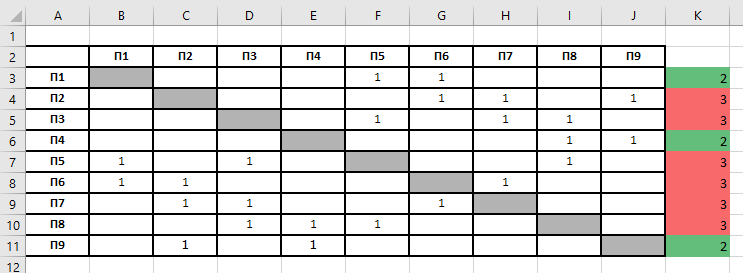
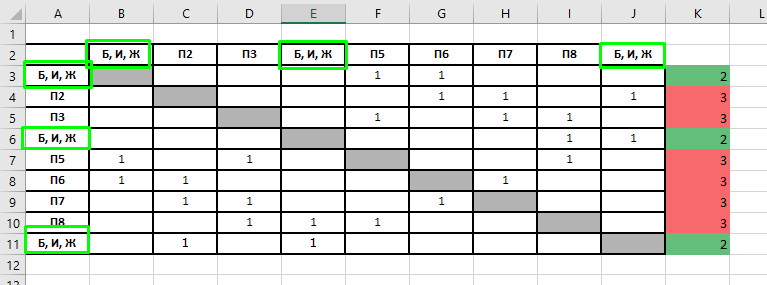
Результат подсчетов можно посмотреть на рисунке ниже:
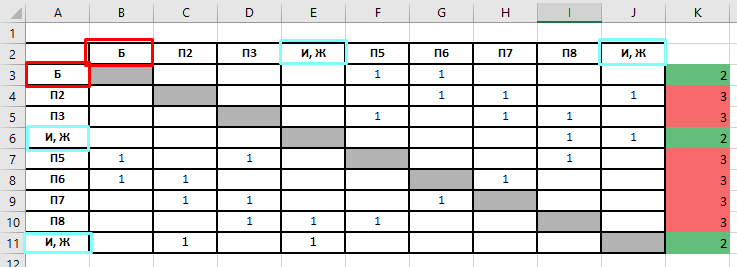
Видим, что три вершины имеют связность 2 (выделены зеленым). Это П1, П4 и П9. И шесть вершин имеют связность 3 (выделены красным).
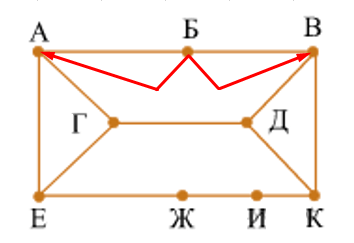
Посмотрим на нашу схему графа. По ней четко видно, что три вершины, имеющие связность два — это Б, И, Ж
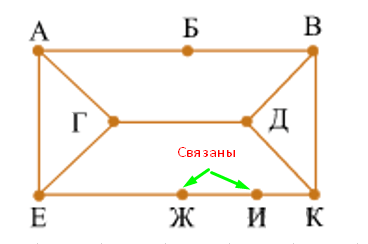
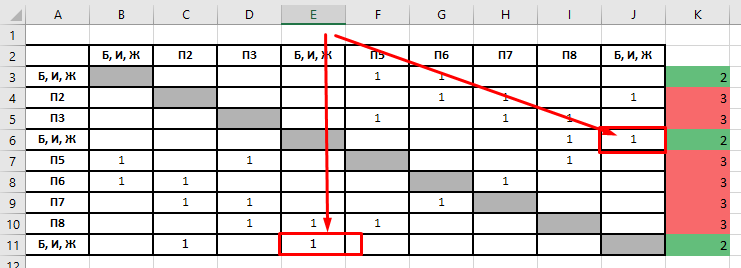
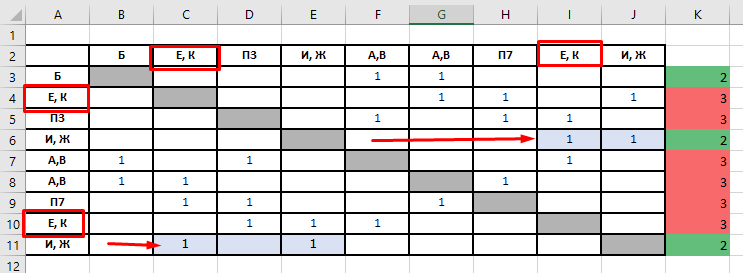
Еще раз посмотрим на схему графа. Можно увидеть, что вершины Ж и И вязаны друг с другом. Найдем в таблице, какие из ячеек Б, И, Ж связаны друг с другом.
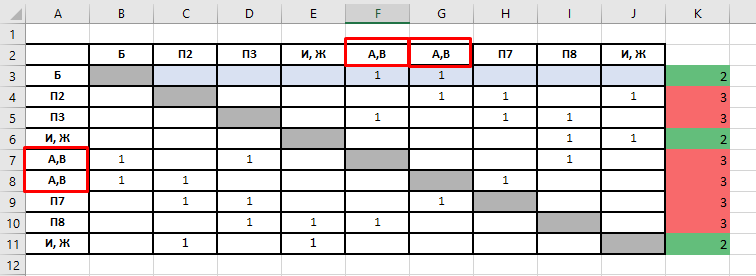
Следовательно, вершина в первой строке таблицы — это Б, а оставшиеся вершины степени 2 — это связанные между собой И и Ж. Отмечаем это в таблице
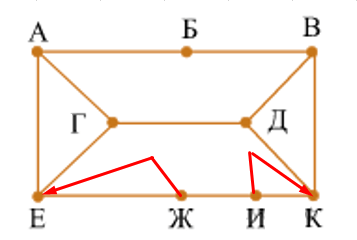
Снова смотрим на граф, и с какими вершинами связана Б. Это А и В. В таблице — это ячейки П5 и П6. Исправляем их название.
Смотрим на графе, с какими вершинами связаны И и Ж. Это Е и К. В таблице — это П2 и П8. Исправляем.
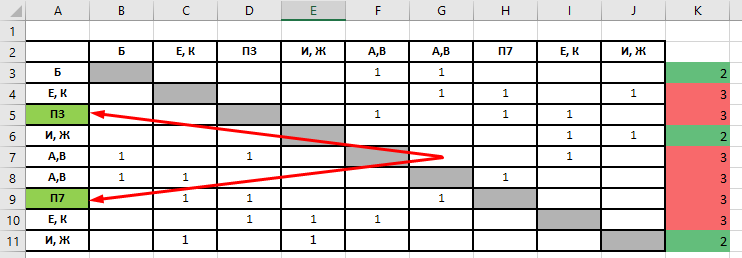
Очевидно, что две оставшиеся до сих пор неизвестными вершины Г и Д, соответствуют данным П3 и П7 таблицы. В ответе необходимо записать только их номера: 3 и 7:
Неоднозначное соотнесение таблицы и графа.
Здесь, также как и в предыдущем задании, необходимо определить соответствие вершин графа на рисунке и в таблице. Но, особенность в том, что для многих вершин — это невозможно сделать. Однако, есть вспомогательные условия, помогающие ответить на вопросы заданий.
Пример задания
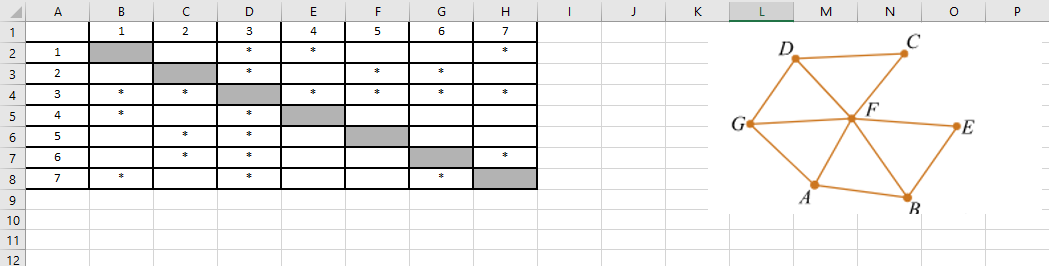
На рисунке слева изображена схема дорог Н-ского района, в таблице звёздочкой обозначено наличие дороги из одного населённого пункта в другой. Отсутствие звёздочки означает, что такой дороги нет.
Каждому населённому пункту на схеме соответствует его номер в таблице, но неизвестно, какой именно номер. Определите, какие номера населённых пунктов в таблице могут соответствовать населённым пунктам A и G на схеме. В ответе запишите эти два номера в возрастающем порядке без пробелов и знаков препинания.
Решение задания
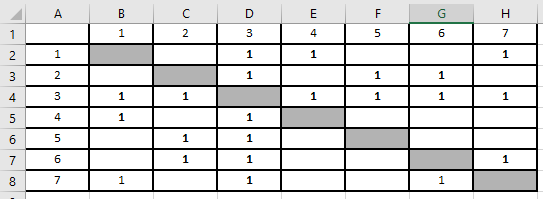
Копируем таблицу и граф в Excel, делаем замену звездочек на символы «1». Как это сделать, описано в предыдущем решении.
Считаем степени вершин графов в таблице через функцию СЧЁТ.
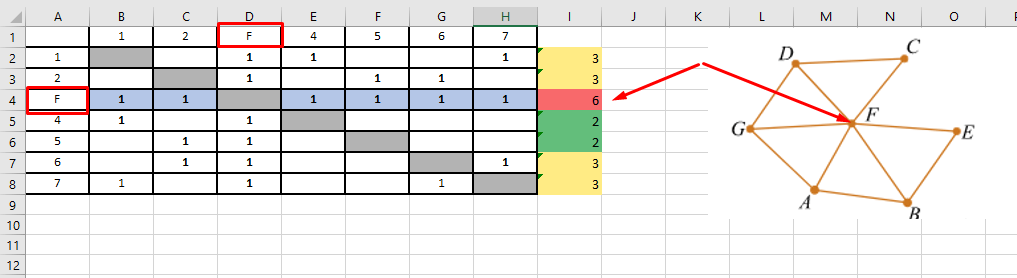
Одна из вершин имеет степень 6 (выделена красным). По рисунку, определяем, что это вершина F. Отмечаем ее в таблице:
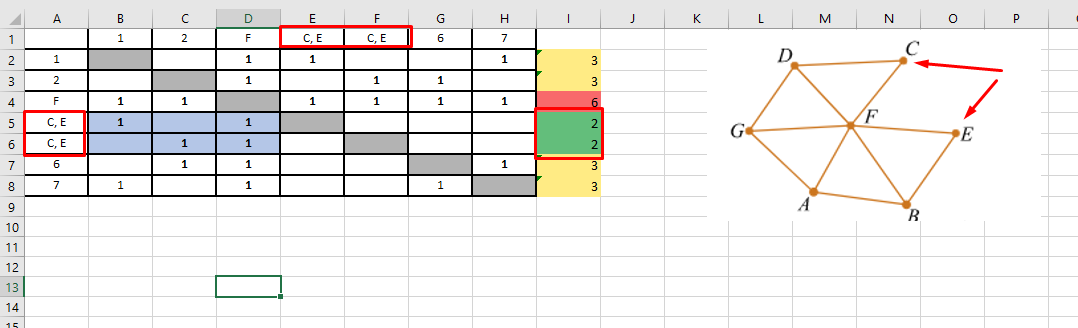
Две вершины (4 и 5) имеют степень 2. На графе мы видим, что — это C и E.
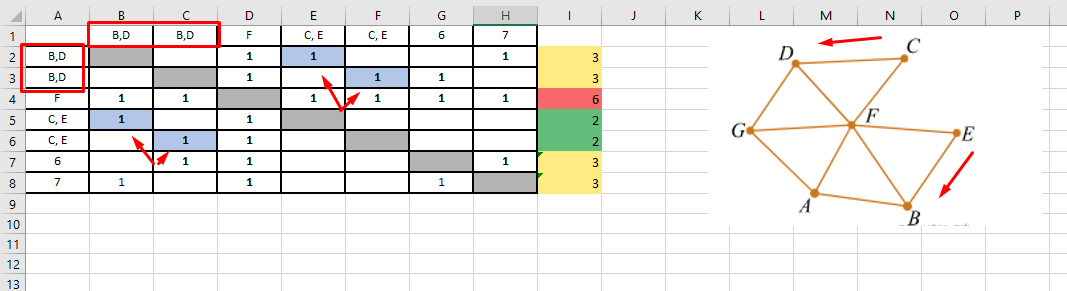
Обе эти вершины (C, E) соединены с вершиной F, а также с вершинами D, B.
В таблице, им соответствуют номера 1 и 2.
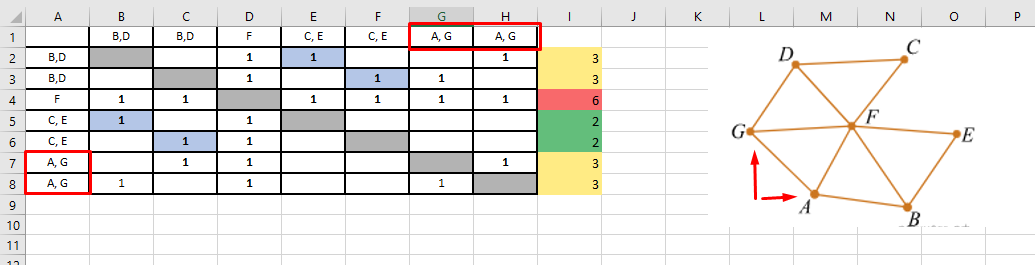
Оставшиеся ячейки, которые идут под цифрами 6 и 7 таблицы — это G и A.
Это и есть ответ на задачу. Вершинам A, G соответствуют ячейки 6 и 7 таблицы.
Видеорешение задачи 1 ЕГЭ по информатике
Для тех, кто не любит читать, видео с нашего канала. Подписывайтесь!

Подготовиться к ЕГЭ с репетитором
Чтобы сдать ЕГЭ по информатике на высокие баллы, нужно владеть следующими навыками:
- Общая теория информации: системы счисления, измерение информации, представление информации, передача информации, логические операции, теория множеств, динамическое программирование.
- Уметь работать в электронных таблицах: Excel или аналоги
- Уметь работать с текстовыми редакторами: Word, Notepad
- Уверенно владеть одним языком программирования: знать основные конструкции, уметь составлять алгоритмы и реализовывать их на алгоритмическом языке.
- Уметь работать с файлами, представлять как они хранятся на диске, понимать что такое путь, имя и расширение.
Наша школа готова помочь вам с подготовкой к компьютерному ЕГЭ по информатике. Небольшие мини-группы по 5 человек, индивидуальный подход и темп освоения материала. У нас большой опыт подготовки новичков с нулевыми навыками программирования. Записывайся:
Задача №7.5
Найдите нарушения правил построения сетевых графиков в сетевой модели на рис.7.7.
Рис.7.7. Сетевая модель задачи №7.5
Используя данные о непосредственно предшествующих работах (табл.7.5), перечислите работы, которые неверно отображены на сетевом графике (рис.7.8), устраните найденные ошибки.
Исходные данные задачи №7.6
Непосредственно предшествующие работы
Рис.7.8. Сетевая модель задачи №7.6
8. РАСЧЕТ И АНАЛИЗ СЕТЕВЫХ МОДЕЛЕЙ
8.1. Теоретическое введение
Календарное планирование предусматривает определение моментов начала и окончания каждой работы и других временных характеристик сетевого графика. Это позволяет проанализировать сетевую модель, выявить критические работы, непосредственно определяющие срок выполнения проекта, провести оптимизацию использования ресурсов (временных, финансовых, исполнителей).
Расчет сетевой модели начинают с временных параметров событий, которые вписывают непосредственно в вершины сетевого графика (рис.8.1):
– ранний срок наступления событияi, минимально необходимый для выполнения всех работ, которые предшествуют событиюi;
– поздний срок наступления событияi, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
– резерв событияi, т.е. время, на которое может быть отсрочено наступление событияiбез нарушения сроков завершения проекта в целом.


- для исходного события И
;
- для всех остальных событий I




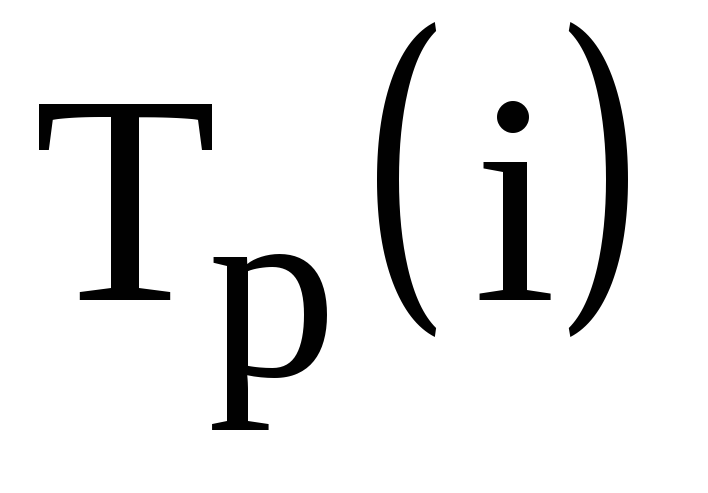

- для завершающего события З
;
- для всех остальных событий





– ранний срок начала работы;
– ранний срок окончания работы;
– поздний срок окончания работы;
– поздний срок начала работы;
– полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы
или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;
– свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы
или отсрочить ее начало, не меняя ранних сроков начала последующих работ.
Путь –это последовательность работ в сетевом графике (в частном случае это одна работа), в которой конечное событие одной работы совпадает с начальным событием следующей за ней работы.Полный путь –это путь от исходного до завершающего события.Критический путь –максимальный по продолжительности полный путь. Работы, лежащие на критическом пути, называюткритическими. Критические работы имеют нулевые свободные и полные резервы.Подкритический путь –полный путь, ближайший по длительности к критическому пути. Для проведения анализа временных параметров сетевой модели используютграфик привязки, который отображает взаимосвязь выполняемых работ во времени. По вертикальной оси графика привязки откладываются коды работ, по горизонтальной оси – отрезки, соответствующие длительностям работ (раннее начало и раннее окончание работ). График привязки можно построить на основе данных о продолжительности работ. При этом необходимо помнить, что работа

Сетевая модель задачи и ее решение.
Изобразим моменты i=1,2. N+1 в виде вершин графа, а пары (i,j) в виде ориентированных дуг этого графа (основные понятиятеории графови терминология приведены в Приложении). Проставим на дугах (i,j) соответствующие стоимости арендыCijи будем считать их длинами этих дуг. Тогда произвольный планможно представить как путь из вершины1в вершинуN+1, а стоимость плана – длиной этого пути. Наоборот, каждый путь указанного вида является планом аренды. Оптимальным планом аренды будет кратчайший путь из1вN+1. Таким образом, задача об аренде оборудования является частным случаем известной задачи о нахождении кратчайшего пути (маршрута) [1,2,4].
Полученный граф (сеть) с заданными числами-стоимостями на дугах называется сетевой модельюзадачи об аренде оборудования, а нахождение оптимального плана (оптимальных планов) аренды как кратчайшего пути на этой сети – решением на сетевой модели.
Найдём путь методом потенциалов[2-3, 6] для бесконтурных сетей.
На 1-м этапе находим потенциалы— числаVi для каждой вершиныi, означающие кратчайшие расстояния от вершиныiдо конечной вершиныN+1. Потенциалы найдем, начиная с последней и далее по убыванию номеров вершин по формуле

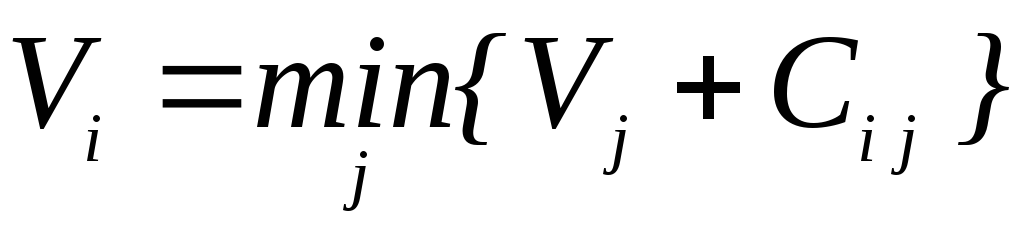
минимум берётся по всем дугам (i,j),выходящимизвершиныi .
На втором этапе, начиная с вершины i=1, находятся и выделяются дуги (i,j), на которых потенциал начала дуги
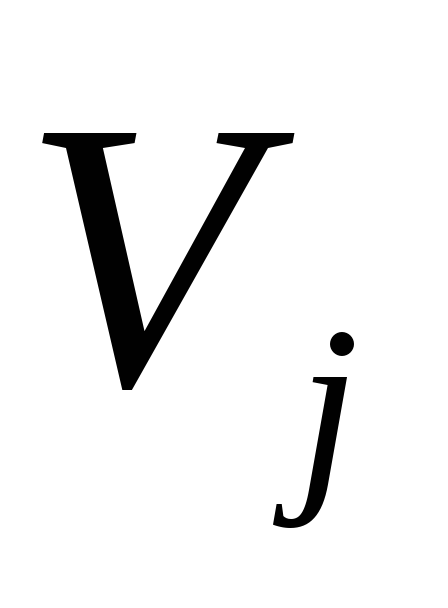

Пример 2. . Пусть при N=6 стоимости аренды Cij заданы в таблице:
j





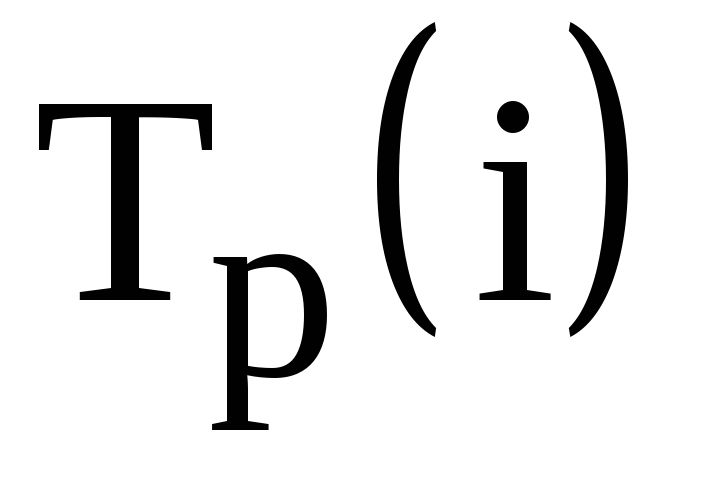 – ранний срок наступления событияi, минимально необходимый для выполнения всех работ, которые предшествуют событиюi;
– ранний срок наступления событияi, минимально необходимый для выполнения всех работ, которые предшествуют событиюi; – поздний срок наступления событияi, превышение которого вызовет аналогичную задержку наступления завершающего события сети;
– поздний срок наступления событияi, превышение которого вызовет аналогичную задержку наступления завершающего события сети; – резерв событияi, т.е. время, на которое может быть отсрочено наступление событияiбез нарушения сроков завершения проекта в целом.
– резерв событияi, т.е. время, на которое может быть отсрочено наступление событияiбез нарушения сроков завершения проекта в целом. ;
; ;
; – ранний срок начала работы;
– ранний срок начала работы; – ранний срок окончания работы;
– ранний срок окончания работы; – поздний срок окончания работы;
– поздний срок окончания работы; – поздний срок начала работы;
– поздний срок начала работы; – полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы
– полный резерв работы показывает максимальное время, на которое можно увеличить длительность работы  или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом;
или отсрочить ее начало, чтобы не нарушился срок завершения проекта в целом; – свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы
– свободный резерв работы показывает максимальное время, на которое можно увеличить продолжительность работы  или отсрочить ее начало, не меняя ранних сроков начала последующих работ.
или отсрочить ее начало, не меняя ранних сроков начала последующих работ.